为什么庞加莱猜想如此难以理解?

庞加莱是有史以来世界上最伟大、最有创见的数学家和物理学家之一。他差一点抢在爱因斯坦之前发现狭义相对论。他几乎是凭一己之力创建了现代数学的一个极其重要的分支——代数拓扑学。庞加莱知识广泛,成就斐然,其研究涵盖了数学的好几个分支,以及天体力学、现代物理学甚至心理学,因此他被称为世上最后一位伟大的科学全才。
庞加菜很像黎曼,喜欢从基本原理出发,开展自己的研究工作,而不是把研究建立在其他人的成果甚至自己先前的工作之上。现今大多数数学家认为他是有史以来最伟大的天才之一。他还对数学思维的本质有着一种浓厚的兴趣。1908 年,他在反省自己思想过程的基础上,作了关于数学创造性的著名演讲,题目为“数学的发明”。
庞加莱自己写道∶“我们通过逻辑去证明,通过直觉去创造。”他尤其不赞同希尔伯特的观点∶数学推理能被公理化并(在原则上)被“机械化”。这是一个庞加莱认为不可能成功的计划,后来哥德尔证明他是对的。
庞加莱对数学的第一个重大贡献是创立了自守函数的概念和理论,这是一类从复数到复数的特殊函数。在他随后的生涯中,庞加莱对涉及复数的函数作了进一步的研究,人们普遍把他誉为多复变解析函数理论的创建者。他还研究了数论和几何学。
庞加莱猜想
在庞加莱对拓扑学的研究中,产生了一个世界难题∶庞加莱猜想。1895 年,庞加莱出版了他的著作《位置分析》。在这本书中,庞加莱引进了拓扑学中的几乎所有的概念和主要方法。
拓扑学是一种“超几何”。数学家通过拓扑学研究曲面和其他数学对象的非常一般的性质。在拓扑学中,数学家的兴趣大都集中在三维或更高维的数学对象上,庞加莱错误地认为某个关于二维物体很显然的事实对于三维或更高维的类似对象也会成立(这是庞加莱猜想的来源)。
二维拓扑学有时被很有联想性地称为“橡皮膜几何学”。
橡皮膜几何学
1931 年,英国的贝克设计了现在的伦敦地铁。这张地图被认为是最好地图之一,很多人试图对它进行改进,都没有成功。这张地图把方便性与外表的美结合在了一起,现在已经成为伦敦的标志,也是全世界地铁地图的典范。
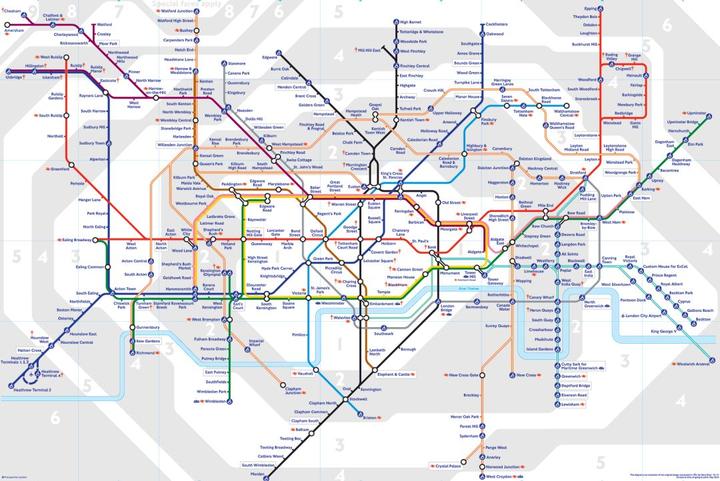
- 拓扑学的应用∶伦敦地铁地图。
这张地图显示出了拓扑学的巨大威力。事实上,这张地图在每一个方面都是不准确的。但它精准地描述了一名乘客需要从这张地图中获取的信息——什么地方上车,什么地方下车,什么地方换线,从而而牺牲了其他所有的细节。
这个例子说明了二维拓扑学的本质。如果把那张地铁地图印在一张具有极好弹性的橡皮膜上,它就可以被拉伸和压缩得使每个细节都正确,从而形成一张标准的、地理上准确的地图。用数学术语说,原因在于这个网络结构(定义为由不同直线连接的点的集合)的布局是一个拓扑性质。简单地说,网络是拓扑对象。你可以扭曲和拉伸一个网络中的任何连线,而不会改变其总体布局。要改变这个网络,你必须断开一条连线或增加一条新的连线。这对电路图、电路本身、计算机芯片、电话网络和互联网都成立。
这就是为什么当今世界上“橡皮膜几何学”是最重要的数学分支之一。在地铁地图的情况中,只要它在拓扑上是准确的,制图上是不是准确没有关系。类似地,对于电路或计算机芯片的设计,重要的是网络的布局。如果布局在拓扑上是准确的,那么电线的位置可随意改动,以满足其他的设计要求。在计算机芯片的设计中也是如此,关键是蚀刻在硅片上的电路必须在拓扑上是准确的。

一般说,二维拓扑学(橡皮膜几何学)是研究图形的这样一种性质∶把这图形画在一张(假想的)具有极好弹性的橡皮膜上,然后扭曲和拉伸这张膜,这种性质仍然保持不变。其实,拓扑学的发展不是由任何应用数学领域的需要驱动的。相反,它来自纯粹数学的内部,来自于想理解微积分为什么有效而进行的奋斗。
微积分与拓扑
从牛顿和莱布尼茨在 17 世纪中叶发明微积分的那一刻开始,数学家就广泛地使用了它。但是,没人真正理解为什么微积分会有效。在一大批数学家长达 300 年的努力下得到了(他们对实数和无穷过程的本性,以及数学推理本身进行了详细的分析),这终于得到了解释。
但这也让数学变得越来越抽象了。19 世纪出现了大量的新类型对象和模式,它们不属于日常经验的任何一部分。在最近 200 年间数学家研究的新对象和新模式中,有非欧几何(平行线可以相交)、四维和更高维的几何学、无穷维几何学、用符号代表图形对称性的代数(称为群论)、用符号代表逻辑思维的代数(命题逻辑),以及用符号代表二维或三维空间中运动的代数(向量代数)。
在抽象性的扩增中,拓扑学也随之出现了。一开始想法是发明一种“几何学”,来研究图形不会被连续变形所破坏的性质,因此这种几何学不依赖于直线、圆、立方体这些概念,也不依赖于长度、面积、体积、角度这些度量。在拓扑学中,研究的对象称为拓扑空间。
拓扑学与“微积分怎么会有效”之间的联系十分微妙。在本质上,这两者都依赖于能把握无穷小。但是拓扑变换与无穷小会有什么关系?这关键就是∶从直观上说,拓扑变换的本质是,两个在变换前“无限靠近”的点,在变换后仍然保持“无限靠近”。特别是把一张橡皮膜无论怎样拉伸、压缩或扭曲,都不会破坏这种靠近性。一开始相互靠近的两个点在操作完成后还是保持靠近。
注意,这里所说的靠近的概念是相对于拓扑空间中所有其他点而言的。我们可以拉伸这张膜,使得两个起初紧靠在一起的点在我们看来不再紧靠在一起。但是在这种情况下,“靠近性”的变化是一个我们从外部施加的几何变化。从橡皮膜的角度看,这两个点仍然是紧靠在一起的。
破坏靠近性的唯一方法是割破或撕开这张膜——这是一种在拓扑学中被禁止的操作。
要发展拓扑学,数学家必须找到一种方式来把握相对靠近这一关键思想。为此,他们着手寻找一种能阐明两点“无限靠近”这一假设性概念的方式。直观上说,拓扑变换具有这样的性质,
如果两个点一开始是无限靠近在一起的,那么在进行了这种变换之后它们仍将如此。
这种方法的问题在于“无限靠近”这个概念不是一个定义良好(well-defined)的概念。然而,通过这种方式来考虑拓扑变换,数学家找到了一种能给拓扑变换下一个精确定义的方式(别指望我在这里给出定义)。这时,就可以用拓扑变换的概念来精确地分析“无限靠近”这个直观概念。通过这种方式,他们在一种严格的意义上发展了微积分。
这就是庞加莱和其他数学家创立拓扑学的主要原因。第一次遇到拓扑学的人心中会产生一个问题∶关于拓扑空间。拓扑空间不仅没有直线,也没有固定形状的概念,更没有任何类型的距离。你所能说的只是什么时候两点相互靠近。
你没有想到的还有很多

拓扑学是当代数学中最丰富多彩、最有魅力和最重要的分支之一,在数学、物理学和其他领域中有着许多应用。这里只提一个重要的应用∶拓扑学是超弦理论的数学基础,而超弦理论是关于宇宙本质的最新理论。
让我们看一看拓扑学家研究的东西。为简单起见,我只限于二维的情况。并思考一下高中几何中有什么性质可以转移到拓扑学中。因为拉伸和扭曲橡皮膜将把直线变成曲线,并改变距离和角度,所以这些我们熟悉的几何概念在拓扑学中毫无意义。
那么还剩下什么呢?还有线和闭圈(环)。如果你在一个具有极好弹性的橡皮膜上画一个圈,那么不论你如何拉伸、压缩和扭曲这张橡皮膜,这个圈仍然是一个圈。还有什么呢?
为回答这个问题,我给你们看看第一个拓扑学成果。它归功于瑞士大数学家欧拉。1735 年,欧拉解决了一个长期悬而未决的难题——柯尼斯堡桥问题。柯尼斯堡的许多市民习惯与家人一起来此散步,他们常常要走过好几座桥。于是有了一个经常讨论的问题∶是不是有一条路线,正好每座桥只走过一次?
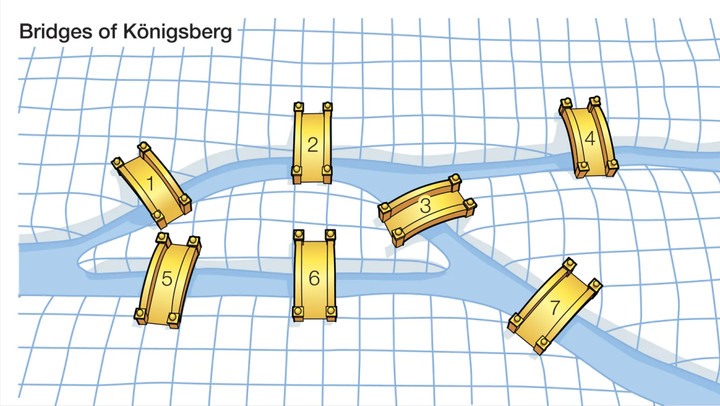
欧拉意识到岛和桥的准确位置是无关紧要的,重要的是这些桥的连接方式,也就是说,由桥形成的网络。这个问题是一个拓扑学问题,而不是几何学问题。
于是欧拉论证如下。取任何一个网络,假设有一条行进路线,正好每条边只走过一次。任何一个结点,只要不是这条路线的起点或终点,必定有偶数条边在此相交,这是因为这些边可以按一条路进一条路出的方式配成对。但是在这个由桥组成的网络中,那 4 个顶点都是有奇数条边在那里相交。因此不可能有这样的路线。结论是,经过柯尼斯堡的每座桥正好一次的路线是不存在的。
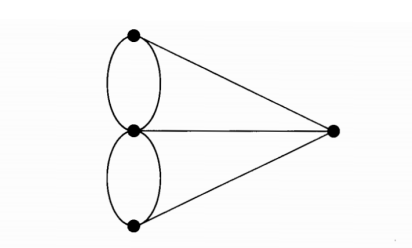
- 网格的结点代表陆地
这个对柯尼斯堡桥问题的解答产生了世界上第一个拓扑学定理。欧拉证明了对于画在平面上的任何一个网络,如果 V 是顶点(结点)的总数,E 是边(或连线)的总数,F 是"面"(由 3 条或更多条边围成的封闭区域)的总数,则下面这个简单的公式成立∶
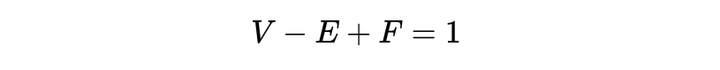
例如,关于柯尼斯堡桥的网络,有 V=4,E=7,以及 F=4,于是
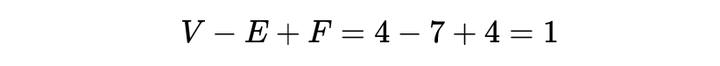
虽然欧拉解决了第一个拓扑学难题,并证明了第一个拓扑学定理,但是直到 19 世纪后期,拓扑学才真正起步。因为在这时,庞加莱登场了!
透过表面
在拓扑学中,我们研究图形和对象在一种连续变形下保持不变的性质。所谓连续,我们是指这个变形不涉及任何切割、撕裂或黏贴。
例如,在拓扑学中,橄榄球与足球是一样的,它们和网球也是一样的,因为这三种球的任何一种都可以通过连续变形而变成其他两种。在拓扑学中只存在一种“球”。平时我们识别出来的各类球之间的差别,都与大小和形状有关,但这些都不是拓扑性质。
拓扑学的早期研究就是寻找各种方式来说明两个形状什么时候在拓扑上是不同的,庞加莱就是这种探求的一个领军人物。
例如,虽然任意两个球都是拓扑相同的,任意两个环面(圆形状、椭圆形状或其他什么形状的)也是拓扑相同的,但任何球面与任何环面是拓扑不同的。从直观上看,这好像是显然的。毕竟,你好像根本没有办法对一个球面进行连续变换而得到一个环面。问题就在于那个无关紧要的词——好像。你怎么知道肯定没有办法做到这一点?例如,
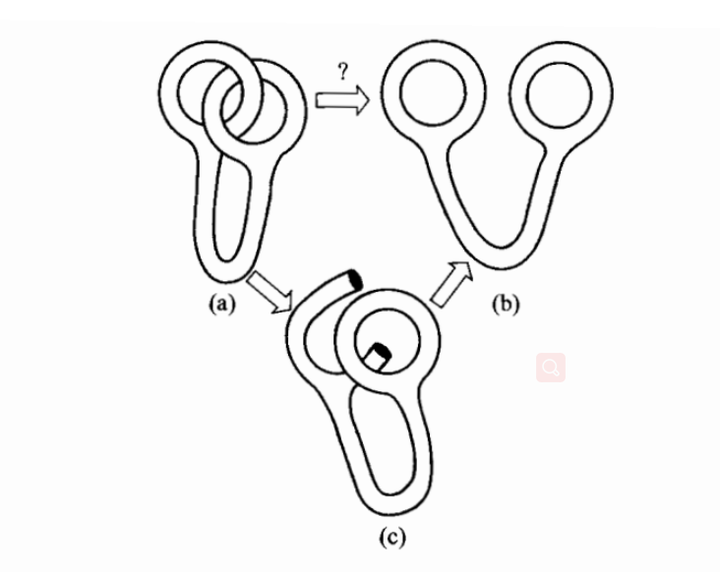
上图所示的分环智力题中,你能不能找到一种方法把图形(a)连续地变换成图形(b)?容易想到的方法是把两个相互扣住的环中的一个割断(但这不被允许),如(c)所示。但不用把环割断也能做到。这应该让你相信寻找各种完全可靠的方式来证明两个对象拓扑相同或拓扑不同,确实是一个重要的任务。
顺便说下,仅凭没能找到一个把一个对象变成另一个对象的连续变形,是不能确证这两个对象拓扑不同的。这里需要的是找到两个对象中一个具有而另一个不具有的某种拓扑性质——即经过连续变形仍保持不变的性质。
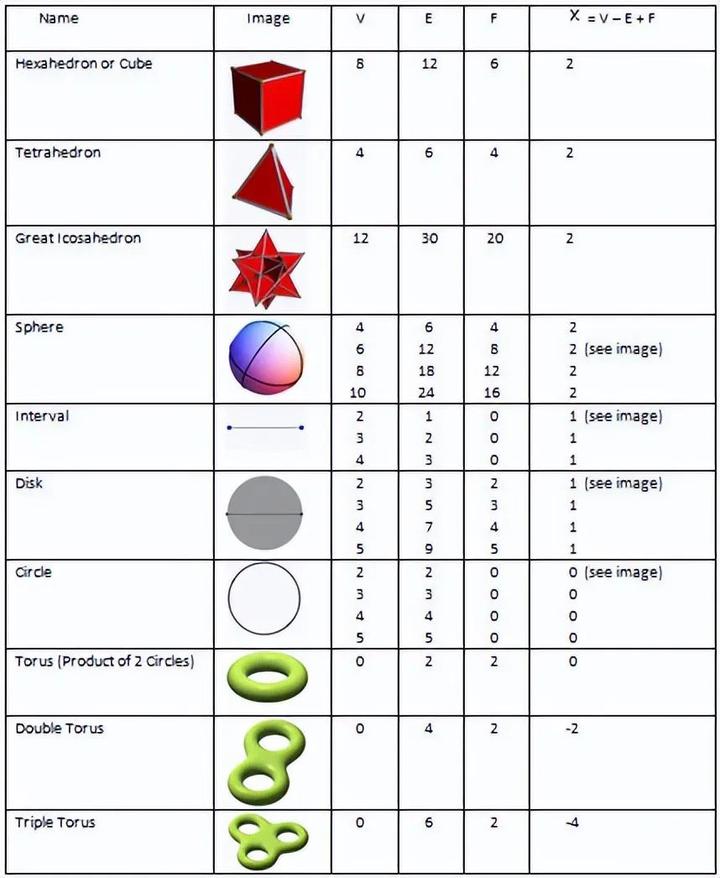
我们已经遇到过一个这样的性质。对于任何网络,V - E+F 的值就是一个拓扑性质。这个量对任何网络都相同。
对于二维平面上的网格,V - E+F=1;对于球面上的网络(要覆盖整个球面,而不是覆盖球面的一部分),V-E+F=2;而环面上的网络(同样要求覆盖整个环面),V-E+F =0。于是,我们可以绝对有把握地断言,二维平面、球面和环面是拓扑不同的。对于画在双环面(形状如数字 8)上的网络,V-E+F=-2,所以我们还知道双环面与平面、球面、环面是拓扑不同的。
对于画在一个特定曲面上的任意网络,表达式 V-E+F 的值是数学家所谓的曲面拓扑不变量的一个例子。如果我们对这个曲面进行拓扑变换(即连续变形),这个值将保持不变。为了纪念欧拉的贡献,人们把 V-E+F 的值称为曲面的欧拉示性数。拓扑学家已发现了许多可用来确定两个特定曲面是否拓扑等价的拓扑不变量,欧拉示性数是其中之一。
另一个拓扑不变量是一个曲面的色数。它起源于一个关于地图着色的经典问题。1852 年,一个名叫格思里的青年英国数学家提出了一个似乎无足轻重的问题∶
为了能在任何一张地图上给各个区域着色,你至少需要多少种颜色?
唯一的规则是任何两个共有一条公共边界的区域必须被着上不同的颜色。(如果两个区域仅在一点相互接触,那么这个点不能被看作是公共边界。)很容易画出需要四种不同颜色的地图,然而是不是存在需要五种颜色的地图?答案是否定的,但数学家花了 100 多年时间才证明了这一点,证明涉及的不仅有巧妙的数学推理,而且有计算机的重大应用。事实上,四色定理是第一个被认为要使用计算机才能得到证明的数学猜想。

四色定理显然是一个拓扑学结果,因为对画有地图的纸进行连续变形,不会改变共有边界的模式。在变形前共有一条公共边界的两个区域,在变形后仍然如此,反之亦然。
四色定理,以及它所回答的那个原始问题,都是针对画在平面上的地图的。但是你可以对画在任何曲面上的地图提出同样的问题。一个曲面的色数是,对画在这个曲面上的任何地图都能进行着色所至少需要的颜色种数。根据四色定理,平面的色数是 4。球面的色数也是 4。环面的色数是 7。
有侧性问题
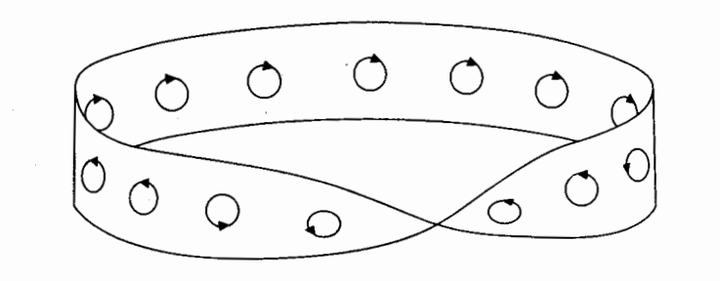
另一个拓扑不变量起源于“有侧性”(sidedness)的概念——一个曲面有一个侧面还是有两个侧面。任何曲面都是有两个侧面,不是吗?回答是否定的。很容易构造一个只有一个侧面的曲面。拿一条狭长的薄纸带,把它扭转半周,然后把两端黏合在一起,形成一个扭曲的纸圈,

这个扭曲的纸圈就是仅有一个侧面的曲面,它叫做莫比乌斯带。除了仅有一个侧面外,默比乌斯带也只有一条边。
默比乌斯带这个例子告诉我们,有侧性是与有边性紧紧联系在一起的。通常,数学家关注没有边的曲面——他们称之为闭曲面。而且,更为有趣的拓扑性质都与曲面的内部结构(曲面是怎样扭曲和翻转的)有关。事实上,对每个有一条边或多条边的曲面,一般存在一个几乎具有相同性质的闭曲面。例如,一个球面和一个有限平面(如平坦的桌面)就性质相似,当我们证明了一个关于球面的拓扑结果,通常立即就有了关于平面的一个结果,反之亦然。
从直观上说,这是因为我们可以取一张完全可拉伸的平纸,然后把它的边缘收拢,形成一个封闭的袋子————在拓扑学上这就是一个球面。
与默比乌斯带相对应的闭曲面叫做克莱因瓶。克莱因瓶没有边缘,而且既没有内部也没有外部。从理论上说,你可以取两个默比乌斯带,沿着它们那条单一的边把它们黏合在一起,就形成了一个克莱因瓶。我说“从理论上说”,是因为你不可能在普通的三维空间中进行这样的操作。克莱因瓶(作为数学一个对象)仅存在于四维空间。在我们的三维世界中,你最好是允许这个曲面穿过它自身,
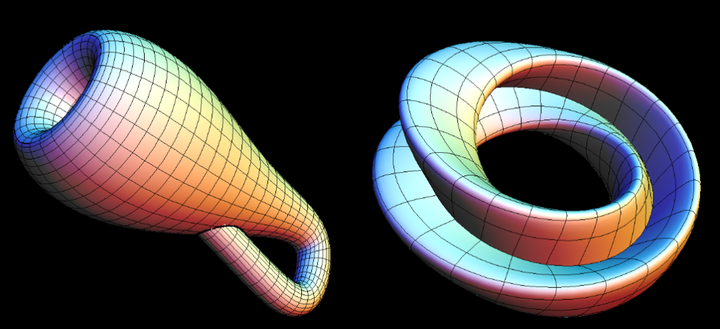
在四维空间中,这个瓶子没有必要穿过它自身。对于普通人来说,一个仅存在于四维空间的对象当然不是真实存在的,但数学家不这么认为。毕竟,每个人都"知道"负数没有平方根,但这并没有阻止数学家创立了复数,并在实际应用中使用它们。数学的许多巨大威力来自于这样的事实∶
我们可以用它来研究超出三维世界中的生物所构想的对象。
例如,我们可以研究画在克莱因瓶上的网络的性质。我们发现克莱因瓶的欧拉示性数是 0,与环面相同。这是不是意味着克莱因瓶与环面是拓扑等价的?不是!欧拉示性数不能区分克莱因瓶与环面,但是色数能,克莱因瓶的色数是 6,环面是 7。
克莱因瓶的“与其表面单侧性相对应的”拓扑性质是一个称为不可定向性的奇特概念。它是指在克莱因瓶的表面上你不能区分左手性与右手性或顺时针旋转与逆时针旋转。如果你在克莱因瓶的表面上画一只的左手,然后把这个图形沿着这表面滑动到足够远(足够远的意思是,如果这个克莱因瓶在三维空间中,那么这只手要完全通过自相交的瓶颈),于是当它返回起点的时候,你会发现它不可思议地变成了一只右手。
这个实验在默比乌斯带上做更为容易。在这个曲面上画一个小小的左手,然后在其临近复制出这个图形,重复这个过程,直至回到你的起点。这时你会发现这只左手变成了右手。或者,在克莱因瓶的表面上或默比乌斯带上画一个小圆圈,用一个箭头表示顺时针旋转,如果你沿着曲面滑动或复制这个图形,直至你返回起点,这时你会发现这箭头指向逆时针方向了,
不能通过沿曲面滑动把左手变成右手或把顺时针变为逆时针的曲面被称为是可定向的。例如,球面(或平面)是可定向的,环面和双环面也是如此。一个能够做到上述改变的曲面,比方说克莱因瓶或默比乌斯带,被称为是不可定向的。可定向性(或不可定向性)是一种拓扑不变量。
曲面分类
拓扑学最初的成果之一是证明了只要有欧拉示性数和可定向性这两个拓扑不变量,就能区分任何两个闭曲面。这就是说,如果两个闭曲面有相同的欧拉示性数,而且都是可定向的或都是不可定向的,那么它们事实上是等价的。这个结果称为曲面分类定理,因为它说只要用这两个特征你就能把所有的曲面分类(在拓扑学意义上)。
简单说,曲面分类定理的证明是通过把球面取为基本曲面并估量任一给定曲面与球面的差异程度(即为把球面转变成那个曲面而不得不对球面所做的事)而作出的。这与我们的直觉相一致∶球面是最简单、最基本的闭曲面。

在这种情况下,为把球面转变成某种另外的曲面而对球面实行的操作超出了连续变形这个常规的拓扑操作。确实,如果你通过扭转、弯曲、拉伸和压缩来改变球面,结果得到的对象在拓扑学意义上仍然是一个球面。要弄清楚曲面怎样从球面构造出来以对曲面进行分类,就必须在通常的扭转、拉伸等之外,还允许进行切割和缝合。拓扑学家称这个过程为“割补术”。典型的割补术包括从球面上割下一片或数片,对这些片进行扭曲、翻转、拉伸或压缩,然后把这些片重新缝到球面上。
分类定理告诉我们,任何可定向曲面与一个表面上缝合了一定数量“环柄”的球面拓扑等价。你可以通过在球面上切割出两个洞,再用一根管子把它们连起来而得到一个环柄,如下图左边所示,任何不可定向曲面与缝合了一定数量“交叉套”的球面等价。你可以在球面上切割一个洞,再把一个默比乌斯带缝在这个洞的边缘上而得到一个交叉套,如下图右边所示。与克莱因瓶的情况一样,在普通的三维空间中,不让默比乌斯带穿过自身是不能做成这件事的。
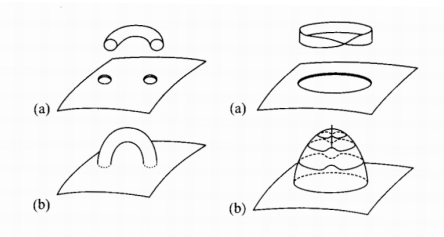
- 曲面分类定理说,任何光滑闭曲面与带有一定数量环柄或交叉套的球面拓扑等价。
20 世纪早期,庞加莱和其他数学家着手对曲面的高维类似物(他们称为"流形")进行分类。他们尝试的方法类似于那种对二维曲面已经有效的方法。他们取一个球面的三维类似物(称为“三维球面”)作为基础,并估量任一三维流形与这三维球面(简称 3- 流形)的差异程度,以设法对所有三维流形进行分类。
注意,一个常规的曲面,如球面或环面,是一个二维对象。虽然这个曲面所包围的部分是三维的,但这曲面本身是二维的。
除了平面之外,任何曲面只能在三维或更高维的空间中构造。于是,任何闭曲面都需要三维或更高维的空间。例如,构造一个球面或一个环面就要取一个三维空间,构造一个克莱因瓶就要取一个四维空间。然而,一个球面、一个环面或一个克莱因瓶都是二维对象——一个没有厚度的曲面,在原则上可以用一张平坦的具有极好弹性的薄片做成。
但是正如球面可以看作是圆(它是一种一维对象——曲线,处在二维空间中)的二维类似物(处在三维空间中),我们同样可以设想球面的三维类似物(处在四维空间中)。当然,实际上我们设想不出。但是我们能写出确定这样一个对象的方程,并且在数学上研究它。其实,物理学家通常就是研究这种设想出来的对象,并运用这些结果帮助理解我们所在的宇宙。3- 流形,即曲面的三维类似物(存在于四维或更高维的空间中),有时被称为超曲面,而球面的三维类似物则被称为超球面。

你可以写出确定三维、四维、五维、六维或任何维的流形的方程。物理学家目前研究的关于物质的数学理论把我们所在的宇宙看作有 11 维。根据这些理论,我们直接觉察到的是这些维中的 3 个维。而其他的维则作为各种不同的物理特性(如电磁辐射和把原子结合在一起的力)把自己表现出来。
庞加莱试图通过取各个维的“球面”作为一种基本图形,然后应用割补术,来对三维和更高维的流形进行分类。在这种尝试中,第一步自然是寻找一种简单的拓扑性质,它可以告诉你什么时候一个给定的(超)曲面与(超)球面拓扑等价。
记住,我们在这里做的是拓扑学。甚至在常规二维曲面这种简单的情况中,一个曲面可能表现得极其复杂,但结果仍然能通过连续变形变成一个球面。
在二维曲面的情况中,存在这样的一个性质。假定你取一支铅笔,在一个球面上画出一个简单的闭圈。现在想象这个圈收缩得越来越小,收缩时保持在球面上滑动。这个圈可以收缩到多小是否有个限度呢?显然没有。你可以把这个圈收缩得无法与点区别开来。从数学上说,你可以把它真的收缩成一个点。
如果你一开始是在一个环面上画出一个圈,那么不一定会发生同样的事情。任意画在一个曲面上的圈能收缩到一点的性质是一种只有球面才具有的曲面拓扑性质。这就是说,如果有一个曲面,它上面的每一个圈(“每一个”在这里很重要)都能不离开这曲面而收缩成一点,那么这个曲面与球面拓扑等价。
对一个三维超球面,这一点同样成立吗?这是庞加莱在 20 世纪初提出的问题,这是他通向一个三维超曲面分类定理之路的第一步。他创立了一个系统的方法(称为同伦论),来研究当一些圈在一个流形上移动和变形时这些圈会发生什么情况。
事实上,情况并非如此。起初,庞加莱臆断三维流形的圈收缩性质确实是三维球面的特征。然而,过了一段时间后,他意识到他的臆断可能不成立。1904 年,他把他的疑问发表,
考虑一个没有边界的三维紧流形 V,即使 V 与三维球面不同胚,V 的基本群是不是也可以是平凡的?
降维说就是,
一个具有圈收缩性质的三维流形是不是可能不与三维球面等价?
庞加莱猜想就此诞生!
1960 年,美国数学家斯梅尔(Stephen Smale)证明了对所有五维和五维以上的流形,庞加莱猜想是正确的。这样,如果一个五维或更高维的流形有这个性质,即画在它上面的任何闭圈可以收缩成一点,则这个流形与同维的超球面是拓扑等价的。
遗憾的是,斯梅尔使用的方法不能运用到三维或四维流形,因此原初的庞加莱猜想仍然未能解决。后来,在 1981 年,另一个美国人弗里德曼发现了一种方法,证明了关于四维流形的庞加莱猜想。
问题还没有解决。庞加莱猜想已被证明对每一维都是正确的,除了三维。斯梅尔和弗里德曼由于他们的成就,都获得了菲尔兹奖。首先证明庞加莱猜想的这个唯一余留情况的人无疑将获得同样的荣誉。
2003 年,俄罗斯数学家格里戈里·佩雷尔曼证明了庞加莱猜想的三维情形,2006 年,数学界最终确认佩雷尔曼的证明解决了庞加莱猜想。
[新春采购季]阿里云 服务器2核2G 61元起/年 点这里优惠购买
[新春采购季]腾讯云 云服务器2核2G 61起/年 点这里优惠购买
感谢您的来访,获取更多精彩文章请Ctrl+D收藏本站。

本文为【软件乐园】原创文章
转载请附上原文链接:https://app.qiip.cc/archives/488
本网站的文章部分内容可能来源于网络,仅供大家学习与参考,如有侵权,请联系站长删除处理。
本站一切资源不代表本站立场,并不代表本站赞同其观点和对其真实性负责。
本站一律禁止以任何方式发布或转载任何违法的相关信息,访客发现请向站长举报
本站资源大多存储在云盘,如发现链接失效,请联系我们我们会第一时间更新。

共有 0 条评论