6 个碳原子能够组成 C6 分子吗?
前言
六个碳原子可以组成什么东西?如果是限定有机物,而且可以随便补足氢,那么只要按照有机物的结构规则,从链烷烃开始不断减小饱和度,穷举每一个分子式的异构体即可。但是如果只有 6 个碳原子,那形成的团簇(cluster)会有哪些结构?这令人想起某经典题目:把原子摆放在球面上,使得任意两个原子之间的距离总和最大——但是要注意,团簇结构不是一个简单的空间几何问题。涉及成键的问题连力场都无法描述,枉论简单的 toy model。不同元素的电子结构、原子大小、成键能力千差万别,最终并不一定都能收敛到某几个看似完美的高对称型结构。
如果将 C6 团簇的一个结构看作 18 维空间里的一个点,每个结构可以映射到一个能量值;在基态时,这个结构只能在基态的势能面上移动,那么本题实际上就转化为一个全局优化问题。由于总共的自由度太高、搜索空间太大,我们在搜索结构时会采取各种算法,以及利用原子的化学物理特性作为约束条件,来尽可能包括所有具有物理意义的结构,而少得到一些无意义的 xjb 摆的结构(比如原子们互相距离无限远……)。团簇全局优化有很多成熟的程序,比如马老师组的 CALYPSO、李老师组的 TGMin、敝组的 pgopt 等等……但由于本题只涉及 6 个原子,我们将采取最简便粗暴,也是最容易上手的一个免费程序:genmer(by sobereva),来进行团簇的结构搜索。
本文所有计算在调用四核情况下总耗时大约 4 小时,家庭 PC 可以完成。
结果与讨论
- 为了生成较紧凑的团簇结构,且在给定的搜索空间内尽可能充分取样,我们设置键长为 vdW 半径的 1.5 倍,并限定每个原子距离团簇质心的最大距离为 3 Å,使用 genmer 总共生成 1000 个结构。耗时 1 s。
- 为了筛除不合理结构、重复结构与不稳定结构,我们使用 xtb 在 GFN2-xTB 下对生成的所有结构进行粗优化。由于半经验方法的势能面与高级电子结构方法得到的存在区别,为了避免结构都收敛到 GFN2-xTB 的局部最低点导致后续计算的 sample 不足,我们对每个结构只进行五步优化,只要稍微朝着更有化学意义的方向爬几步即可。耗时 ~5 min。
- 使用 molclus 对粗优化之后的结构进行去重,使用的阈值为 1 kcal/mol 与 1 Å,筛选之后剩下 138 个结构。接下来在 B3LYP-D3/6-31G* 下采用 loose 收敛标准进行几何优化。这一步的目的是让前一步通过半经验粗优化的结构能跑到附近的 DFT 势能面的局部极小值附近,从而便于去重与减少下一步的计算量。耗时 ~2 h。
- 再次对 初步 DFT 优化的结构进行去重,使用的阈值为较严格的 0.25 kcal 与 0.1 Å,筛选后剩下 20 个结构。对于这 20 个结构在 B3LYP-D3/6-31G* 下采用 tight 收敛标准进行较严格的几何优化。跑完后再次去重,只剩下 10 个结构。耗时 ~30 min。
- 最后,对这十个结构在 B3LYP-D3/6-31G* 下进行振动分析,确认无虚频(即为势能面上局部极小值),并且算出室温下的自由能热矫正。然后在 DLPNO-CCSD(T)/def2-QZVPP 下计算他们的高精度电子能量。耗时 ~1 h。加上热校正,得到了高精度的吉布斯自由能(该方法得到的自由能精度可达到 ~0.1 kcal/mol,堪称单参考方法天花板),如下:
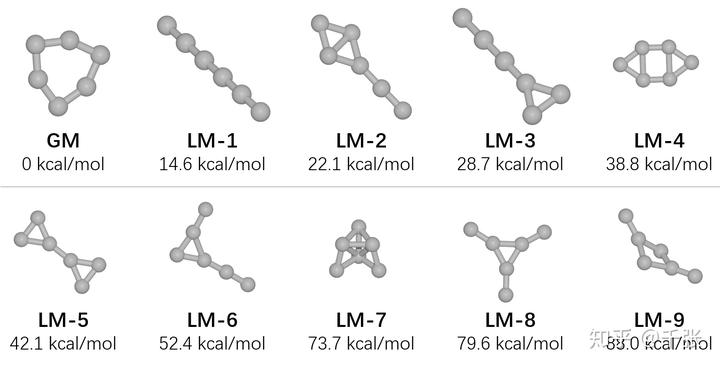
很可惜,题主想要的正八面体结构不在其中。其实在粗优化后有一个结构特别接近八面体,但是在 DFT 等级的优化时它就断键崩溃成了 LM-7 结构,估计是张力过大瞬间爆炸。
再来仔细看看得到的各个团簇结构,一直学(背)唯象理论的人估计头皮发麻:这都什么玩意儿?论对称性,GM 是一个 D3h 的压瘪的六元环,LM-1 就是一根光棍儿,之后也是各种牛鬼蛇神,并且对称性极低的 LM-6 居然比 LM-8 还稳定???论化学键,这些结构里没几个碳是连了四个原子的,即使连了也离正四面体差得远……为了理解其中的成键模式,接下来让我们选取其中几个结构来进行化学键分析。
GM,全局最小值结构。看起来似乎就是光秃秃一个环,但其实其中大有玄机。图里画的每个碳原子只成了两个键是因为我直接基于共价半径来判断成键与否,但常规的价键理论根本无法描述 GM 里存在的化学键。首先,沿着环一圈儿存在 σ 键,然后明眼人也可以看出来六个碳共面,z 方向 p 轨道共轭出的大 Π 键。查看了一下分子轨道,果然有:
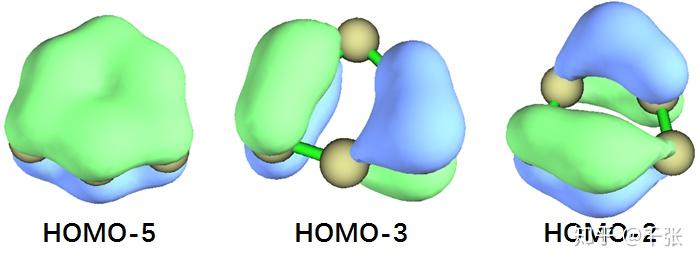
如图可见,HOMO-5 就是一个完美的离域 Π,虽然 Π 也有反键轨道被电子占据,但是只有 HOMO-3 和 HOMO-2 而已,并没有完全反掉这个 Π。另外,这里的碳并不是苯那样的 sp2 杂化,所以这两个被占据的轨道对于 GM 中 Π 的反键作用与苯中的 Π* 有差别。
另外我们还可以看到这样的分子轨道:
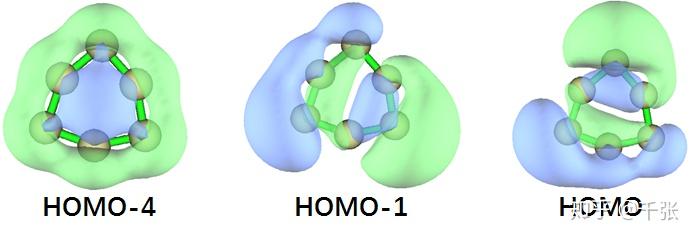
即,xy 面内的 p 轨道一端指向环内、一端指向环外,形成了环内外侧的 Π 键。这个实际上有点类似于 sob 老师提到过的 C18 环。为了详细分析这两种 Π 的强度,我们分别对于平面内外的 Π 轨道电子可视化了 LOL 空间分布,并且计算了他们的多中心键的键级:
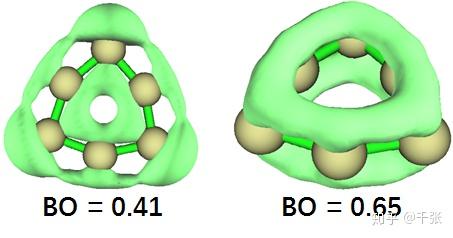
可见环内外的 Π 由于空间上的错位,p 轨道重叠不足,键级要稍弱于传统的 Π。
接下来再看看 LM-1,大光棍的成键情况。HOMO 对于 C1-C2,C3-C4,C5-C6 是 π 成键轨道,但是对于 C2-C3,C4-C5 来说则是反键。HOMO-3 与 HOMO-4 分别是 x 与 y 方向的,C1-C2-C3 与 C4-C5-C6 上的共轭 π。HOMO-5 与 HOMO-6 则分别是 x 与 y 方向是盖 C2-C3-C4-C5 的共轭 π。那是否存在直线上的离域大Π键呢?是也不是。我们可视化了 π 轨道电子的 LOL 空间分布,如下:
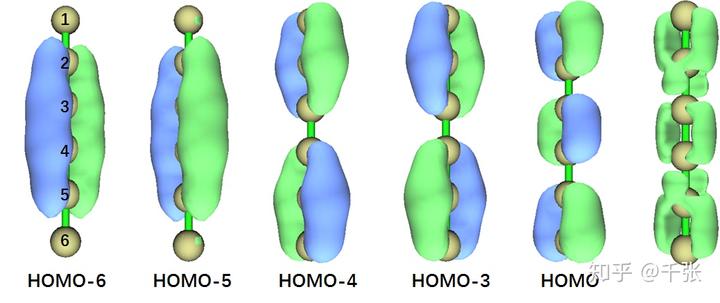
各位朋友第一反应大概会想到累积多烯烃,没错,LM-1 的成键方式与之非常相似:首先 p 轨道沿着 z 方向成一连串的 σ 键,然后 C1-C2, C3-C4, C5-C6 在 y 方向成了较强的 π键,C2-C3, C4-C5 则在 x 方向用多余的 p 电子成了较弱的 π 键。由于两端不像累积多烯烃那样有 H,所以多余电子更多分布在 x 方向的 π轨道上。从等值面来看姑且可以认为是离域了。
而 LM-6 为甚么比 LM-8 要稳定呢?从对称性来看 LM-8 作为 D3h 明显是吊打 LM-6,但是化学键它不是简单的几何问题。由于他们都为平面构象而且 σ 键看起来差别不大,我们直接分析 π 电子的 LOL 分布:
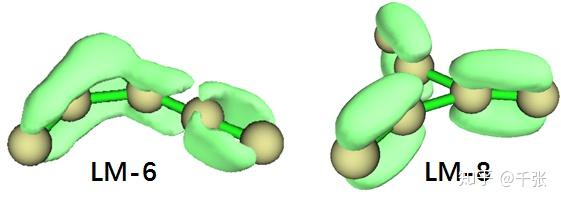
由此可见,LM-8 虽然对称性高,但是 π 电子完全局域化在三个瓣儿的 C=C 上,中间的三角完全没有任何参与;而在 LM-6 中,其中一个碳原子的 pz 轨道被解放,终于在三角区域上形成了离域 Π,而连了两个碳的那一个瓣还喜出望外地在 xy 面内成了一个类似于累积二烯烃的 π 键,也可纳入离域体系。这两重作用直接导致 LM-6 比 LM-8 稳定了好几十 kcal/mol。
而 LM-7 就不好分析了,里面存在大量的超共轭效应(hyper-conjugation),C-C σ 键和 p 轨道疯狂重叠,在笼子里形成了一大坨乱七八糟的东西,难以对 σ 和 π 进行分别讨论 = = 那么就只分析这么几个了,剩余的结构各位读者可以留作课后练习(?
结论
- 6 个碳可以组成 C6,本文找出来了 10 个稳定结构。可惜题主想要的正八面体他不稳定。
- 一点私货:亚纳米尺度的团簇拥有违背常识与化学直觉的结构,尤其是其中一些离域化的、非指向性的化学键,用经典的唯象理论难以描述。在研究团簇的过程中,我们对化学键的理解与分析手段也得到了前所未有的发展。如我老板所说,Sub‐nano cluster is the last frontier of Inorganic Chemistry. 再往下深挖的话,我们还可以去研究 C6 团簇不同局部极小值结构之间的异构化动力学、物理性质的差异、化学反应性的区别、异构化过程与化学反应过程的耦合。为此我们需要更高效的电子结构计算方法、动力学取样手段、系综水平对体系的描述 以及做化学应用的更大脑洞。
(补充阅读:年初发的一片 Accounts)
程序
(均为免费或存在免费替代,支持全平台)
[新春采购季]阿里云 服务器2核2G 61元起/年 点这里优惠购买
[新春采购季]腾讯云 云服务器2核2G 61起/年 点这里优惠购买
感谢您的来访,获取更多精彩文章请Ctrl+D收藏本站。

本文为【软件乐园】原创文章
转载请附上原文链接:https://app.qiip.cc/archives/834
本网站的文章部分内容可能来源于网络,仅供大家学习与参考,如有侵权,请联系站长删除处理。
本站一切资源不代表本站立场,并不代表本站赞同其观点和对其真实性负责。
本站一律禁止以任何方式发布或转载任何违法的相关信息,访客发现请向站长举报
本站资源大多存储在云盘,如发现链接失效,请联系我们我们会第一时间更新。

共有 0 条评论