最多可以找到几阶的汉字正交拉丁方阵？

我是题主，我可以讲讲这道题的数学背景。

首先，有一个拉丁方阵(Latin square)的概念：

一个 n*n 的方阵，其中用到了 n 个元素，并且每行、每列的元素都不相同，则构成一个 n 阶拉丁方阵，简称 n 阶拉丁方。

以下是从 2 阶到 6 阶的一些拉丁方的例子：

2 阶：  [0 1]  [1 0]    3 阶：  [0 1 2]  [1 2 0]  [2 0 1]    4 阶：  [0 1 2 3]  [1 2 3 0]  [2 3 0 1]  [3 0 1 2]    5 阶：  [0 1 2 3 4]  [1 2 3 4 0]  [2 3 4 0 1]  [3 4 0 1 2]  [4 0 1 2 3]    6 阶：    [0 1 2 3 4 5]  [1 2 3 4 5 0]  [2 3 4 5 0 1]  [3 4 5 0 1 2]  [4 5 0 1 2 3]  [5 0 1 2 3 4]  

显然，任何阶数都可以构成拉丁方。数独游戏就是一种加强版的 9 阶的拉丁方：

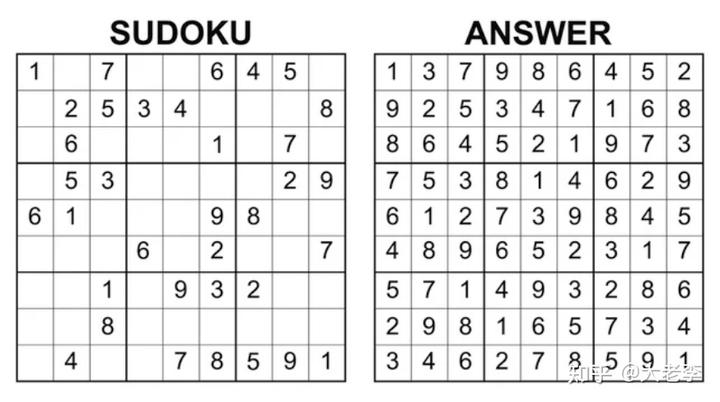
下一个概念是：互斥正交拉丁方阵(Mutually orthogonal Latin squares)。把若干个同阶的拉丁方叠合在一起，取每个原先拉丁方中同一位置的元素，有序排列后，放入新的拉丁方的对应位置中，就是正交拉丁方。

如果正交拉丁方中的所有元素不同，则称为互斥正交拉丁方。也因为多数情况下，互斥正交拉丁方比较有意思，所以一般就简称为正交拉丁方。本文中，“正交拉丁方”也都是指“互斥正交拉丁方阵”。

而如果是两个拉丁方阵构成的正交拉丁方，也被称为希腊 - 拉丁方（Graeco-Latin squares）。以下是 3、4、5 阶的希腊 - 拉丁方的例子：

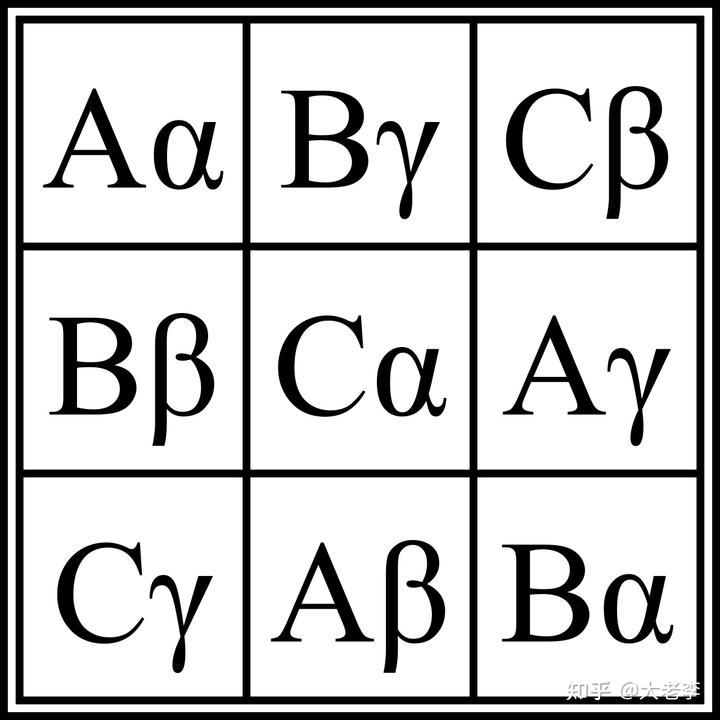
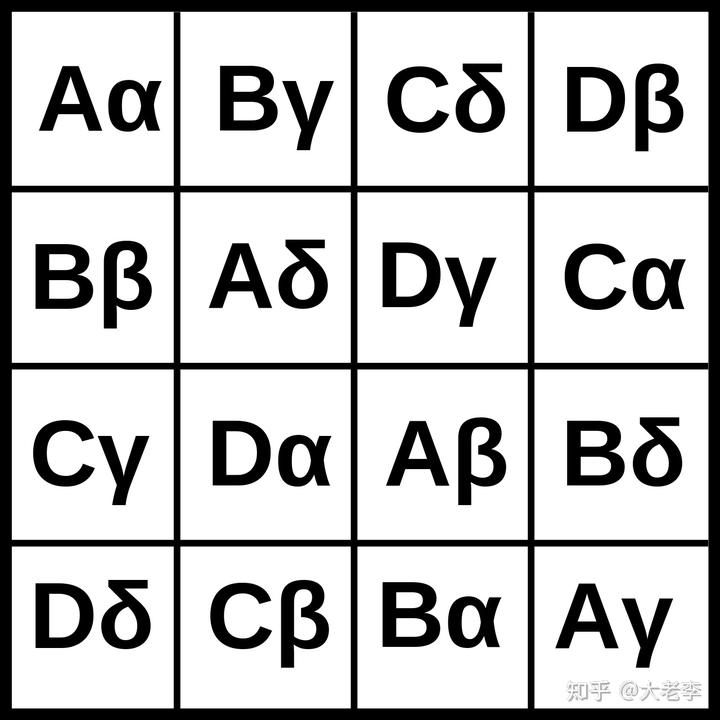
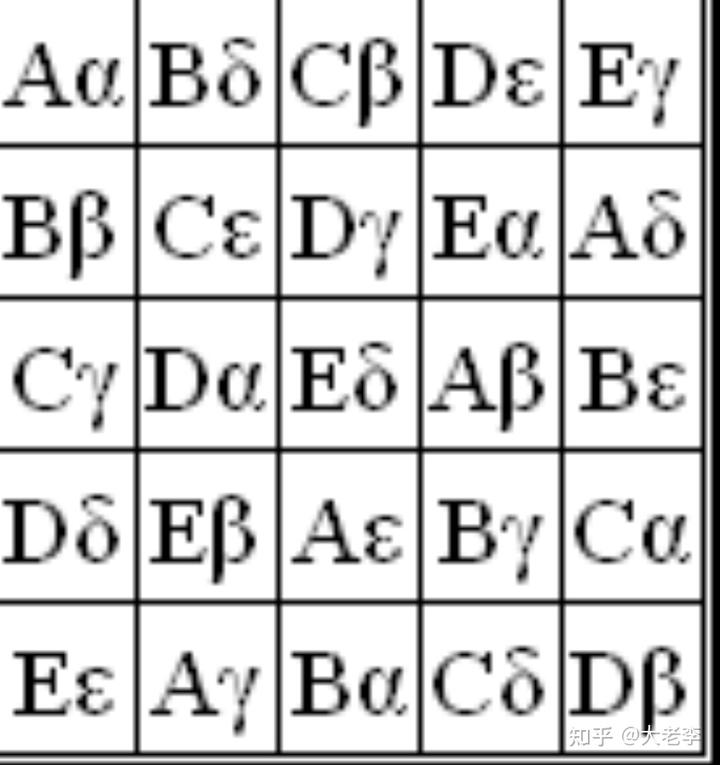
它们是用英文字母和希腊字母的拉丁方正交所得。可以看到，其中没有重复的字母组合。而以下未加说明的话，我们所说的正交拉丁方都是两个拉丁方的组合，即希腊 - 拉丁方。

以下两个 7 阶拉丁方可以组合成一个正交拉丁方：

[0 2 4 6 1 3 5]  [0 3 6 2 5 1 4]  [6 1 3 5 0 2 4]  [5 1 4 0 3 6 2]  [5 0 2 4 6 1 3]  [3 6 2 5 1 4 0]  [4 6 1 3 5 0 2]  [1 4 0 3 6 2 5]  [3 5 0 2 4 6 1]  [6 2 5 1 4 0 3]  [2 4 6 1 3 5 0]  [4 0 3 6 2 5 1]  [1 3 5 0 2 4 6], [2 5 1 4 0 3 6]  

可以验证，以上两个矩阵对应位置数字组合后，没有重复的。

为什么跳过 6 阶的呢？因为确实不存在。

1770 年，欧拉提出了这样一个问题：

一个非常有趣的问题，这个问题已经让许多人的消耗了长时间的智慧，使我参与了以下的研究，这些研究似乎开辟了一个新的分析领域，特别是组合研究。这个问题围绕着如何安排 36 名来自 6 个不同团队的军官，使他们在一个正方形中排列，以便在每一行（横向和纵向）中都有 6 名不同军衔和不同团队的军官。

该问题现在被称为欧拉的“三十六军士”问题。欧拉发现他无法构造出 6 阶和 10 阶的正交拉丁方。2 阶的正交拉丁方显然不存在，于是欧拉猜想：当 n 为除以 4 余 2 的整数时，不存在 n 阶的正交拉丁方。

1901 年，法国人 Gaston Tarry 通过枚举（!）的方法，证明了不存在 6 阶正交拉丁方。但后面的情况出现了意外。1959 年，R.C. Bose 和 S. S. Shrikhande通过数学方法，构造出了 22 阶的正交拉丁方。紧接着，沿着他们的思路，有人利用当时的计算机，构造出了 10 阶的正交拉丁方：

从而彻底推翻了欧拉的猜想。现在正确的结论是：除了 2 阶和 6 阶，其他各阶的正交拉丁方都存在。

而多个正交拉丁方组合在一起，就可以做出更好玩的事情。一个有意思的考察是，对 n 阶，最多可以有几个拉丁方组合成正交拉丁方，该数值被记作 MOLS(n)，其中 MOLS 就是 mutually orthogonal Latin squares 的缩写。

该数值的前 20 项是：

       0   1   2   3   4   5   6   7   8   9  10  11  12  13  14  15  16  17  18  19      ________________________________________________________________________________    0| +oo +oo   1   2   3   4   1   6   7   8   2  10   5  12   4   4  15  16   5  18  

n=2 和 6 时，MOLS(n)=1，意思就是 2 阶和 6 阶的拉丁方只能单独一个，无法再组合成正交拉丁方。

表中可以看到 5 阶时，最多可以有 4 个拉丁方组合为正交拉丁方，于是有人做了这张图。

你可以检查，图中，每个单元格中的字母，字体，前景颜色和背景颜色都不相同。每一行和列中，对应的四个要素也都不相同。

用中文也可以玩，比如 3 个四阶拉丁方组合：

而汉字经常可以拆成两部分，于是我想到了原问题中的这样一道题。现在，看到已经有人找到了 11 阶的汉字希腊拉丁方，这意味着汉字可以进行数独游戏：

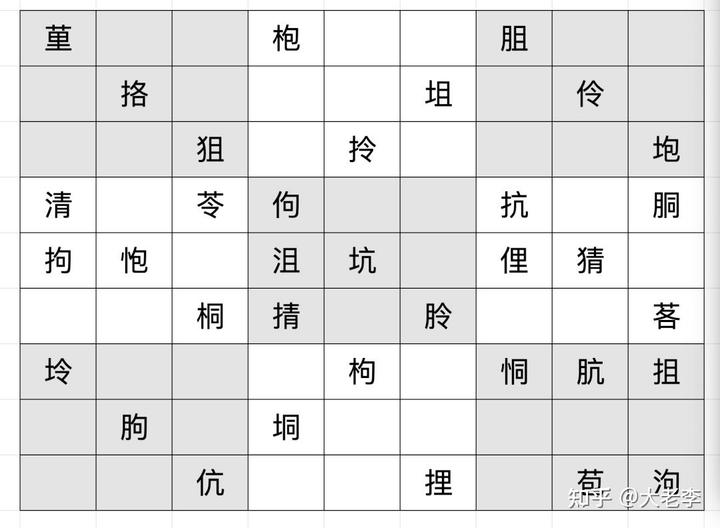
其答案是：

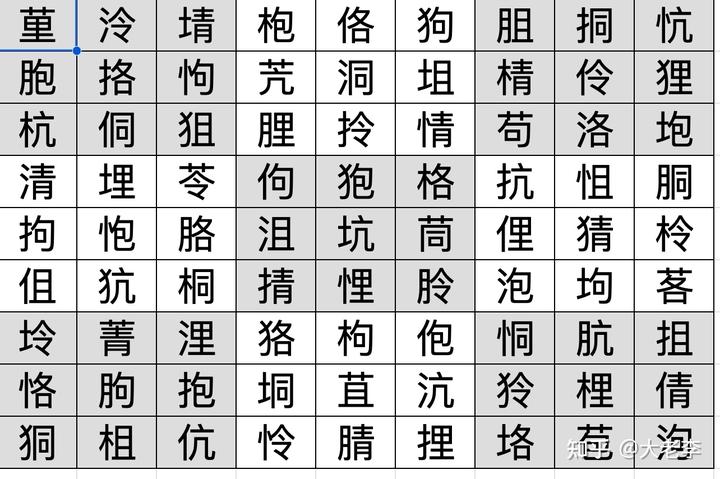
构建此游戏的要点是，需要先找到“正交数独”。构造 9 阶的正交数独并不容易，我没有在网上找到现成的程序。幸而网上找到了一些现成的例子，于是构造出了上题。我也希望有人能写出在线的汉字数独游戏，会非常有意思。

关于此题的背景，就介绍到这里。