抽象代数、同调代数、交换代数、代数拓扑有什么关系？

2021.11.28 对抽象同伦论部分做出大改，感兴趣的话可以直接下拉。这个回答比较粗略的版本是：Grothendieck 的 Tohoku 以及他对同伦论的贡献。

我觉得这几个学科的关系或许真的可以梳理一下(还可以添加代数几何)，同时我觉得这个任务是很有意思的，虽然会有点艰难。这篇文章很长，我尽量把能梳理的东西都梳理一遍，算是给这半年的学习一个总结。

以下都是 1950s 以前的内容，要看更现代的内容，可以往下拉。

1950s

首先最基础的是抽象代数，它为代数提供了最最基础的语言，现在群环域这些结构是几乎所有方向的人都应该知道的，包括一些分析的方向。本科教学阶段，这门课程讲群环域是毫无争议的，但后面主要讲 Galois 理论还是着重 module 这有争议，知乎上已经有这样的问题了，好像浙大那边是着重了 module，不过一般学校还是讲 Galois。

如何评价在抽象代数 I 以模为教学内容？

虽然 Galois 理论是抽象代数的起源，但是不知道 Galois 理论丝毫不影响你对抽象代数的理解，事实上 Galois 理论对数论方向的影响可能会更大一点。

假如想要更快地接近代数领域的话可能还是讲 module 比较合适，因为这个对象是非常常见的，而且直接是向量空间的推广。而 Galois 理论在没有其他基础的情况下很难进行深一步的教学，一般人其实也很难在第一次学 Galois 理论的时候把握到它的核心思想，只会觉得它好厉害，可以解决多项式方程零点问题。后续深入的有关 Galois 的内容，比如 Galois descent、Galois cohomology 等等都不是直接学了 Galois theory 就可以看的。

代数拓扑跟同调代数的关系前期很深。说到代数拓扑跟同调代数的起源，最早可以追寻到 homology 这个概念，它是庞加莱提出来的，但是那个时候它的代数色彩还不浓厚因为最开始它是为了研究在特定空间里面曲线积分的情况。至于 homology 的前身是 Betti number，那时候是黎曼的工作，然后 Betti 进行了一定的改良，但都不成熟，直到庞加莱给出了可行的定义，让 homology 变成了一个空间的不变量。但是我们直到 1930s 才发现 homology 是一个群，这个是 Noether 发现的，这时候才真正有了代数拓扑的雏形。

事实上，就在代数拓扑这个学科里面，那个时候不同子领域，它们对 homology 的定义也是不一样的，像 simplicial homology, cellular homology, singular homology 之类的。这些概念直到 Eilenberg 跟 Steenrod 才统一，在他们的专著里面他们给出了几个公理，一个子领域里面满足这些公理的同调理论是同构的，或者说一个同调理论可以被这些公理充分特征化。

另外代数拓扑里面还有另一个跟 homology 齐名的概念——homotopy，这个也是拓扑空间的不变量，它是同胚的弱化。为了给不同的拓扑空间分类，我们需要这些特征量。拓扑空间的同胚是一个很强的条件，它能实现的情况很局限，而同伦不一样，现实中很多看起来不太一样的两个对象或许可以通过连续的形变变成另一个，这种连续形变的观点抽象了就是 homotopy。有句话，homology 是人为了的代数化，而 homotopy 是空间自带的代数结构。

传统代数拓扑里面有两个很重要的问题，一个是 extension problem，另一个是 homotopy lifting。像 fibration、cofibration 这样的概念都是为了表述跟解决这一系列的问题。古典时期，同伦的发展始终慢于同调，因为同伦是 nonabelian 的，而同调是 abelian 的，这两个的差别在同伦代数跟同调代数里面表现的更明显。因此这个时期同伦的发展在向同调靠拢，同调里面的理论在同伦里面一般有弱化的形式，比如同调的长正合链对应同伦的 fiber sequence。

另外代数拓扑一个长期的任务就是计算球面同伦群，这个也是稳定同伦的任务。比如 Serre 获得菲尔兹奖的原因就是他在求球面同伦群上的重要贡献，他使用的方法是 Eilenberg-Maclane space 跟谱序列。他研究兴趣的转向是他获奖之后的事情。

下面附上这段时间的代数拓扑学家以及他们做出主要贡献的时间点：

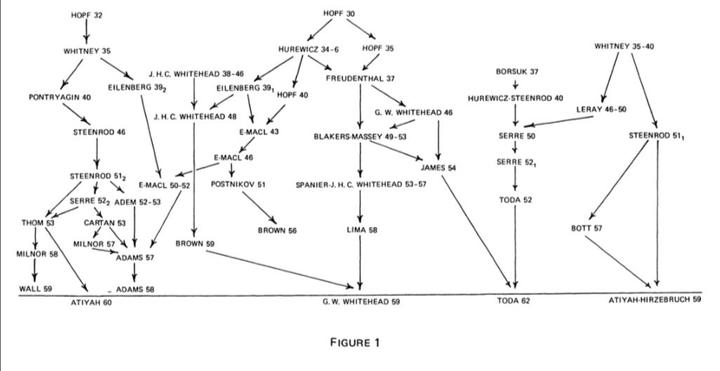
这些大概是 1960 以前的情况，等下讲讲现代的代数拓扑情况(或许没时间)。至于学习古典的代数拓扑教材有非常多，可以看我的文章：

Algebraic Topology I: 对教材跟概念的一些论述

代数化后的同调其实就是一个 complex 里面的 ker/im。同调代数的最初想法可以追溯到 Hilbert，但这是他在研究交换代数时的产物，因此首先我可能得先讲讲交换代数。 Hilbert 他当时研究的主要是不变量理论(这个领域现代的发展是几何不变量，得益于 FGA 里面的 Hilbert scheme 跟 Picard scheme)，并且得到了几个非常非常重要的定理，Hilbert basis、Hilbert Nullstellensatz、Hilber syzygy 等，其中第三个是同调代数思想的萌芽。他当时研究的代数结构主要是 C[X,...,Y]，这个代数结构是典型的 Noetherian 环(这是第一个理论)，这个概念是 Noether 后来总结的，它有几个等价形式。Hilbert 第二个理论有很深的几何背景，是代数基本定理的推广，他把代数对象跟几何对象联系起来，专业地说就是

The category of affine algebraic sets and morphisms (over an algebraically closed field k) is equivalent to the category of affine k-algebras with the arrows reversed.

这些历史背景可以看看 Eisenbud 那本交换代数的第一章。对上面这种代数与几何联系的推广就是现代代数几何的事情了，那段英文翻译过来就是说一般交换环的范畴跟 affine scheme 的对偶范畴等价，这些也可以看看下面的回答跟文章：

Sizhe Chen：学习代数几何前，为何要先学范畴论？

Algebraic Geometry: The Roots of Scheme

第二篇文章其实已经把同调代数的第二个发展阶段讲清楚了，这个阶段的同调代数跟 abelian category 紧紧联系在一起，跟代数几何有很大关系。

Hilbert 第三个有关 syzygy 的理论给出的思想的是不断地追溯你要研究的模的结构。什么意思呢？首先对于一个 module M，有 R^(J) 到 M 的满射，然后再有对这个 kernel 的满射，这样可以一直下去。Hilbert 的这个理论是关于，多项式环下多少这样的步骤后得到的 module 是自由的。syzygy 本意是月球的合冲现象，这里的取名所蕴含的意思是生成元跟 presentation 之间互相“周期性”影响的关系。

这里要提一个很有意思的点，在 R-module 下，R 在 Grothendieck 的 abelian category 的意义下是 generator，即对任何一个模 M 一定存在一个集合 J，使得 R^(J) 到 M 是满射。在一般的 abelian category 下有不一样的等价的推广定义，具体可以看 Tohoku 第一章。这个 generator 的存在是很有必要的，这关系到一个 abelian category 是否有足够的 injective object。这样，Baer criterion 也可以得到推广。如果我没记错的话，满足 Grothendieck 公理 AB 5）的 abelian category 假如有一个 generator ，那一定有足够的 injective object，这样你就可以做上同调了。

Tohoku 其实就是一篇揭示上同调本质的文章，Grothendieck 的很多思想都源于这篇论文。在某种程度上，我觉得 Tohoku 比 EGA 更加重要。

另外在一般的本科交换代数里面，我们会讲 primary decomposition、dimension theory、 integral extension 等内容，这三块是必须要的，同时得注意到这些内容也是有代数数论背景的，不过这些其实只是 1950 以前的内容，交换代数在 1950s 后期、1960s 包括以后有了更大的突破，这些得益于 Grothendieck scheme 理论的突破。其中同调在这个阶段扮演了很重要的作用。

交换代数里面 primary decomposition 是整数上素因数分解的推广，它断言在 Noetherian ring 里面每一个理想都能写成有限个 primary ideal 的交集。primary ideal 是 prime ideal 的推广。dimension theory 主要是 Krull dimension，后面还有用同调定义的几个 dimension，这些个 dimension 在 regular local ring 里面有很融洽的相似性。同时，Krull dimension 也可以反应在拓扑空间上。代数几何里面有 Noetherian space 的说法，一个 affine scheme ，如果它对应的环是 Noetherian 的话，那么它的 ringed space 也是 Noetherian 的，同时拓扑空间上定义的 dimension 跟它的 Krull dimension 相等。

此外 regular local ring 之所以重要，因为在有限生成 k 代数产生的 affine scheme 上面我们可以用这个来定义 smooth 的概念。而一般 scheme 上面要定义 smooth 概念还是比较复杂的，因为流形里面的结论不能直接套用上去。我们首先就得在上面定义一个抽象的微分结构——Kahler Differential，它是一个万有结构。之后为了表述 smooth 的概念，我们需要 Jacobian matrix 以及它的 rank，后者是用来定义 dimension 的，这就是 Jacobian criterion。而在用这套方法判别 smooth 时，我们得首先知道 smooth scheme 的前身—— unramified scheme 非歧化概型，以及非歧化泛射 unramified morphisms 的定义。最后我们达到 etale morphism，这里的 etale 意味着 smooth of relative dimension 0。由于 scheme 跟流形不同，反函数定理在 scheme 上是不成立的，不过 etale morphism 可以看成是局部可逆的泛射。

而对于有限生成 k 代数诱导的 scheme 这种特殊情况，这也是我们最感兴趣的对象，因为各种 algebraic variety 就是指这种情况，我们需要一个方便点的理论，因此利用 regular local ring 我们有

至于 integral extension 则是域扩张的推广，技术性很强，它可以拿来证明希尔伯特零点定理。同时这个东西更多地用在代数数论里面。

有关这个时期的交换代数跟同调代数可以看我的文章：

Homological Algebra and Commutative Algebra

其实这篇文章里面很多东西需要简化跟修改。它里面也讲了第一时期的同调代数，还有交换代数，这些都在那篇文章后面，往下翻就可以了，所以我在此不多赘述了。

以上所有内容都是 1950s 以及之前的，可以算是比较古典的了。

1950s 以后的新发展交换代数：

这里讲讲新的发展，不过限于我的知识水平，讲得肯定会不到位不深入。

首先是交换代数，在 1950s 后期跟 1960s 时期，一个方向是系统研究交换环上不同 dimension 的相融情况。这个在 Topics in the homological theory of modules over commutative rings by Hochster 里面有非常系统的论述，另外这方面会涉及一点集合论的知识，主要是关于基数的。

另一个主要方向是 local cohomology 跟 completion，对于后者它跟点集拓扑里面空间的完备化很像，但很多交换代数都是简单地讲一讲，不深入。而对于前者已经有了很多很好的教材了。

其实这两个都是函子，local cohomology 获得更多的关注是因为它的理论太顺畅了。它的基础函子是 torsion functor，先给定一个环 R 跟它上面的一个理想 I，对于任意一个 R-module M，我们可以定义它的 I-torsion submodule，它由这些 m 构成，存在正整数 n ，使所有的 a 属于 I，有 a^n m=0。这个函子是左正合的，因此它有右导出函子，这些右导出函子叫做 local cohomology functor。它在很长一段时间里面是交换代数研究的中心。

首先它们具有很强的可计算性，Grothendieck 证明了，在 Noetherian ring 上的 module，它们的 local cohomology 可以由 Čech complex 来计算，因为 Noetherian ring 上 finite sequence 是 weakly pro-regular 的。假如我们刚才取的理想 I 是可以由 pro-regular 序列生成的话，那个这个 local cohomology 也可以由 Koszul complexes 计算。

completion 被忽略也是有原因的，从极限的角度来看，torsion functor 是一个特殊的 colimit 函子，但是 completion 函子是一个特殊的 inverse limit 函子，前者的正合性质本身好于后者。虽然 completion functor 是严格地跟 torsion functor 对偶，但是一般来说它没有任何正合性质，除了在几个特殊场合里面。所以对于 completion 我们一般只关注 Noetherian rings 跟 finitely generated modules。Homological Questions in Local Algebra by Strooker 里面讲了很多 adic completion and completeness for non-finitely generated modules 在同调问题上的应用。

下面这张图是 Commutative Ring Theory by Matsumura 里面对现代交换代数历史的简述，里面都是跟同调交织在一起的。

这里面讲的交换代数里面的 flatness，也可以算是一个发展方向，但是它应该算在代数几何里面，因为它主要是关于 descent 的，这在 FGA 里面由 Grothendieck 系统地发展了，在交换代数层面的 descent 可以看我的回答：

Sizhe Chen：如何理解 Descent theory？可以看成基变换的逆过程吗？

另外一个交换代数方向是 Grothendieck duality ，但它跟代数几何的联系非常紧密，甚至跟代数拓扑那边都有关系，毕竟几乎所有对偶理论都是 Grothendieck six formalism 的反应。

代数拓扑：

我觉得代数拓扑这边主要可以分成两类，一类是同伦论的进一步发展，一类是同调论的进一步发展，我们挨个讲，不过这方面我不太熟悉。或许在这之前我们可以先讲讲代数拓扑跟代数几何联姻开始的时期——1950s。

当时代数几何其实跟代数拓扑分界不太明显，因为那时候很多流形都蕴含复代数簇的结构，于是也不用对把代数拓扑的方法用到代数几何里面感到惊奇。最典型的是引入上同调理论，这非常非常成功，我在 the roots of scheme 里面讲过了。但是引入了 homology 怎么能不接着引入 homotopy 呢？在 scheme 范畴上引入同伦理论是 Voevodsky 的主要工作，这在下文有所介绍。

Homology：

其中一个大方向是从 Poincare duality 出发衍生出来的 intersection homology, Borel-Moore homology 跟 Verdier duality。它们用到的工具主要是 constructible sheaf，里面最新的发展有 perverse sheaf(主要跟 singular space 有关)之类的东西。

同调代数方面，它们需要第三个发展阶段的导出范畴跟三角范畴，这些范畴可以拿来更好地刻画对 sheaf 进行各种操作的函子(six formalism)。

传统的 Poincare duality 说假如 M 是一个有向流形，则存在一个同构 D

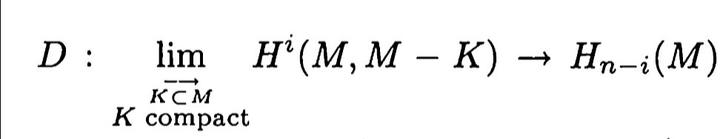
如果 M 不是可定向的，那么给它带上 coefficient Z/2Z，因为方向只有两个，这样也可以得到这个结论。流形的结构是很好的，但在一般的空间里面这个理论显然是不能够成立的。不过在 locally compact space 里面也有很好的对偶性质。

要介绍 Verdier duality 那首先得介绍导出范畴跟三角范畴，然后得介绍函子 f_！跟 f^！，这都不是简单讲解能领会的。其实，两个函子在 locally closed subspace 上性质很好，因为这样可以很简单地证明它们是 adjoint 的，并且 f_!正合。一般情况下：

这些理论简单地说就是，将各种对偶理论搬到导出范畴上，用导出函子来刻画所有的操作，这就让理论变得很简洁。而至于这些操作，其实基本就是 Grothendieck six formalism。

Intersection homology I by Goresky, MacPherson

Intersection homology II by Goresky, MacPherson

Homotopy：

同伦方向 1950s 之后主要是稳定同伦论，这一套理论的发展当时主要是为了计算球面同伦群，值得一提的是里面有一个很重要的概念 spectra，这虽然是稳定同伦里面的概念，但它之后发展出了 ring spectra 的概念，从而应用到了代数几何里面，本质上说它是同伦代数几何很好的模型，同伦代数几何的概念会在下面介绍。

关于稳定同伦的可以看看知乎这个用户的回答跟文章 @梁嘉诚 。

接着附上 1960 左右的图：

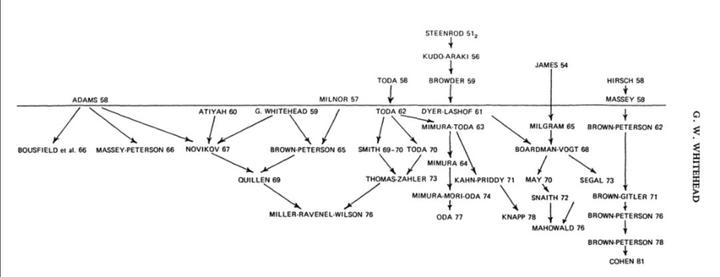
最新的关于代数几何跟同伦论的发展，Voevodsky 的工作(motivic)应该是绕不开的，推荐一下彭柯尧学长的一个回答：

如何评价菲尔兹奖得主 Vladimir Voevodsky？

接下来我们好好讲讲这方面的事情。

首先必须要提到的是 Quillen 在 60s 期间提出的 model category 的概念，这个来自两个启发，一个是 Verdier 的导出范畴，另一个是 Kan 在单纯集合上的工作。那时候大家已经认识到单纯集合范畴跟拓扑空间范畴所定义的同伦理论是等价的。Quillen 系统地回答了这个问题，什么时候两个同伦理论会等价。上面说的 spectra 的范畴，其实也是一个 model category。

上面是代数拓扑侧的，至于代数几何这期间跟同伦论有关的发展是 Grothendieck 的 stack 理论，还有 Giraud 的 gerbes 理论。这些跟非交换上同调的分类理论有关，它具有代数拓扑的思想来源。因为在代数拓扑那里，我们有一个经典的理论，即一个上同调理论可以被一个 Eilenberg-MacLane 空间表示，还有就是一阶的上同调理论可以被 principal bundles 分类。这在代数几何那里是 1 阶的非交换上同调被 torsors 分类，Giraud 部分完成了 2 阶的分类，用 gerbes with liens。那么自然有个问题，高阶的上同调理论该怎么分类？

Grothendieck 在 pursuing stack 里面系统地思考了这个问题，他的想法是把 higher stack 作为参数放进上同调里面，在他的稿子里面 n-stack 是一个到 n-category 或者 n-groupoid 的函子，那么现在的问题自然降解到定义 n-category 的概念了。之后对 n-category 的定义有很多，比较成功是 Segal 定义的 Segal category，这是从代数拓扑出发的，使用的技术是 delooping，虽然 Simpson 是在 Tamsamani 的定义上工作，但是这个定义跟 Segal 的是等价的。因此可以说 Simpson 在 Segal category 上发展了 n-stack 的理论。

而 Joyal，他在给 Grothendieck 的信中首先提出 simplicial sheaf 的概念，也就是单形范畴到 sheaf 范畴的 presheaf。这启发了他后期对 Quasi-category (weak Kan complex) 的发展。

了解到 Joyal 的工作后 Jardine 做出了非常重要的工作，他把目光转向 simplicial presheaf，并且用 local equivalence 作为 weak equivalence，为 simplicial presheaf 范畴找到了它的模型范畴结构，因此它具有一个同论理论。其实可以说，这时候分类上同调理论基本已经完成了，后面的事情大多是在深度发展。

作为 Simpson 的学生，Toen 他们用 simplicial presheaf 的概念发展了 higher stack 的理论，他们把 simplicial presheaf 同伦理论中的对象看成是一个 higher stack，具体的内容可以参看我的这个回答 看 Bousfield Localization 部分。

Toen 他们最重要的研究工作就是发展了一套更加广泛的代数几何——同伦代数几何(HAG)。传统的代数几何是建立在交换环上的，而交换环是 Ab (交换群范畴) 上的“半群对象”(commutative monoid like object)，更严谨地说 Ab 是一个 symmetric monoidal model category，交换环是 Ab 上用范畴定义的“交换半群”对象。scheme 由 affine scheme 粘成，而 affine scheme 的对偶范畴便是交换环范畴。因此更普遍地，我们考虑一个一般的 symmetric monoidal model category，里面的交换半群对象所形成的子范畴，它们的对偶范畴被认为是具有丰富几何信息的某种几何对象的范畴，将它们通过合适的技术(descent)粘起来，那就得到类似于 scheme 的对象。这就是同伦代数几何研究的对象，这种理论也被称为是 higher topos。higher topos 跟 higher stack 的区别就像是 Grothendieck topos 跟 site 的区别。而 HAG 有什么用呢？导出代数几何(DAG)就是它的一个模型。

从代数几何到导出代数几何：复形的几何

从代数几何到导出代数几何：形变与逼近

Lurie 的 derived algebraic geometry 有多重要？

注意 DAG 并不是 Lurie 提出的，而且 DAG 也并不是只有 Lurie 那一个模型，上面两篇笔记中涉及的 DAG 属于另一个 simplicial 的模型，这种模型在欧陆那边更流行，毕竟这种模型就是 Toen 那帮人搞的。

严格来说 DAG 应该起源于 Kontsevich 的 hidden smoothness 原则。他当时在研究有理曲线的计数问题，发现得到的 moduli space 的性质实在是差劲，主要有两方面的问题，首先不是光滑的，其次不具有合适的维度。一般来说模空间反应的是你所研究的曲线的信息，因此他认为这种现象是不寻常的，他猜测他所得到的模空间其实只是真正的模空间(导出模空间)的截断，这样它才显得那么奇怪。DAG 就是研究导出模空间的理论。由于原始模空间的差性质，即切空间不具有稳定的维度，因此这里猜测导出模空间的切空间必须具有稳定的维度，这样那不如直接让导出模空间的切空间变成一条链，这条链上具备了原来不同切空间的信息。

为什么说 DAG 是 HAG 的一个模型呢？因为 DAG 是建立在复形范畴基础上的，复形范畴是一个 symmetric monoidal model category，它上面的 commutative monoid like objet 就是 E_∞-algebra，它所定义的同伦代数几何就是导出代数几何。而实际上，DAG 又有好几个等价的模型，在 Toen 他们那里，他们考虑的模型其实是 simplicial commutative ring，而 E_∞这个表述是非常代数拓扑的，也是 Lurie 采用的观点。

如何理解 E_n algebra?

Lurie 的工作在知乎有些被吹得神乎其神，以至于忽略了 Lurie 的前辈们所作的工作。Lurie 的 higher topos 有好几个思想来源，首先 Joyal 已经有了比较完善的关于 quasi-category 的理论，Toen 他们已经在 simplicial category 上面建立了 higher topos 理论，Rezk 已经有了在 quasi-category 上建立等价的 topos 理论的初步想法了。这些的综合就是 Lurie 的那本 900 多页的关于 higher topos 的书。Lurie 的理论之所以名声很大，我觉得大部分应该归功于 quasi-category 定义的简洁性，可入门性，在它上面的 topos 理论比 Toen 他们的更系统，更简洁，更适合被应用。而 Lurie 后面的 higher algebra 则是对 monoidal category 上的代数模型的推广，以此来发现更加普遍地同伦代数几何形式，这个工作至今还未全部完成。我对这后面的工作了解不多，不好评价。

发现讲到这里都没有提到 Voevodsky 的工作，由于我也不太了解他的工作，因此下面只给出链接。

Voevodsky 的成就之一就是证明了 Milnor 猜想，在证明过程中主要使用的技术是A1-homotopy跟motivic cohomology。