如何直观的感受葛立恒数？

让我们假设我们有一粒沙子

这粒沙子很普通，和广袤沙漠中数之不尽的沙子相比，没有任何特异之处。

它很小，小得几乎看不见。

它是如此渺小，以至于一阵风就能把它吹走。

但它很重要，它是我们的起点。

因为它就是 1，或者说：

理解起来没有任何困难，对吧？

做好准备了，接下来我们要开始向大数领域迈进。

首先是

，或者说一百万。

如果我们把上图的沙子，按照 100×100×100 摆成一个立方体，就能得到下图这样一个沙块。

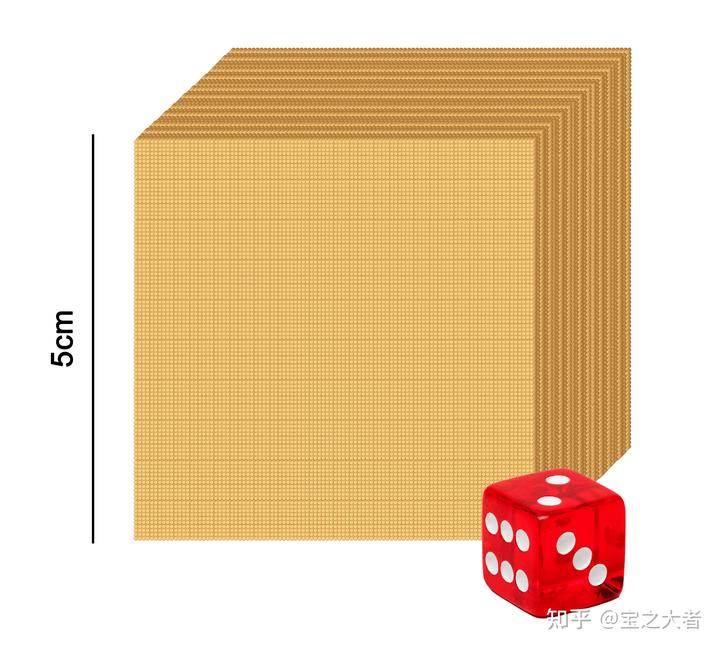
我们一次性跨越了 6 个数量级，沙子也从微观立刻变成了宏观。

但是它还是很小，重量甚至只有 1 斤。

这还不够，远远不够，我们不能在此停留。

这次我们需要

个沙子。

换言之，我们要按照刚刚的办法，把沙块按照 100×100×100 摆放。

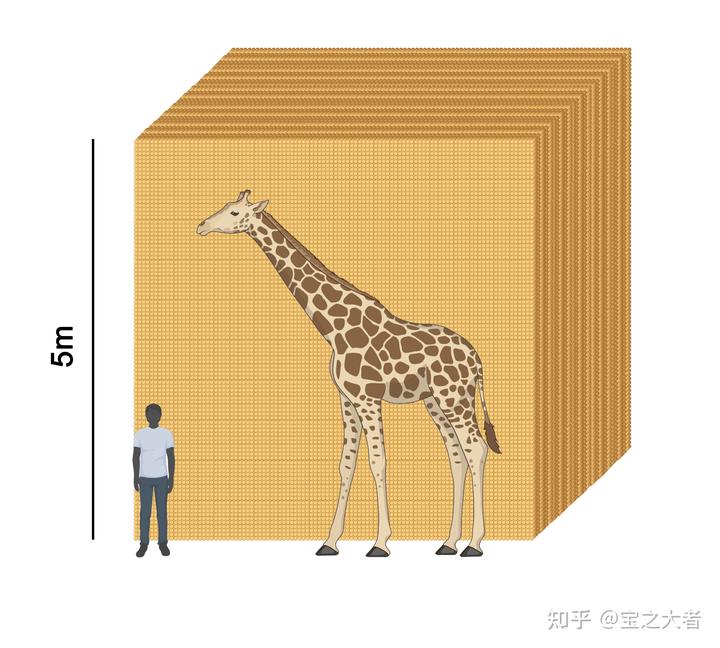
很好，我们的沙子逐渐宏伟了起来。

的沙子，做成沙块时边长足有 5m，这是成年长颈鹿的高度。

这么多沙子，足够在小区里整个儿童乐园了。

值得一提的是，这些沙子重达 500 吨，超过了世界上最重的蓝鲸（180 吨）。

超大型货车载重 30 吨，你得雇 17 辆这样的车，才能装走这么多沙子。

是令人留恋的，毕竟这将是我们最后可以用自己的身体尺度去丈量的地方。

来不及长吁短叹，我们必须启程了，前往

。

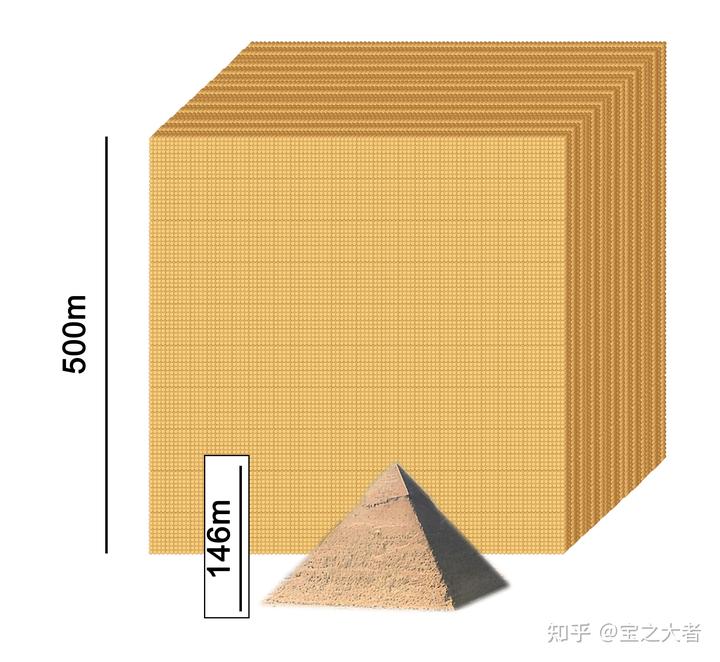
作为一个直径 500m 的巨大沙堡，它的存在本身已经不可能被蓝星上的人类忽视了。

胡夫金字塔高 146m，一向被视为人类九大奇迹之一。

但它在这个沙堡面前显得小鸟依人，仿佛郭敬明站在姚明身畔。

当然了，跟现代文明所建造的个别高楼相比，它还不够高大。

哈利法塔高达 828m，是世界第一高楼，而作为中国第一高的上海中心大厦也有 632m。

但是负责任地说，它的重量 5 亿吨，绝对远远超出侪辈。

哈利法塔据估计也就 10 万吨，毕竟不能使用太重的材料，否则建不了那么高。

其实我们的沙堡已经违背了物理学，因为它没有那么大的结构强度支撑自己的形状。

金字塔造成锥形可不是为了方便千年后的游客参观。

闲言少叙，让我们继续吧，来看看

的沙子是什么样？

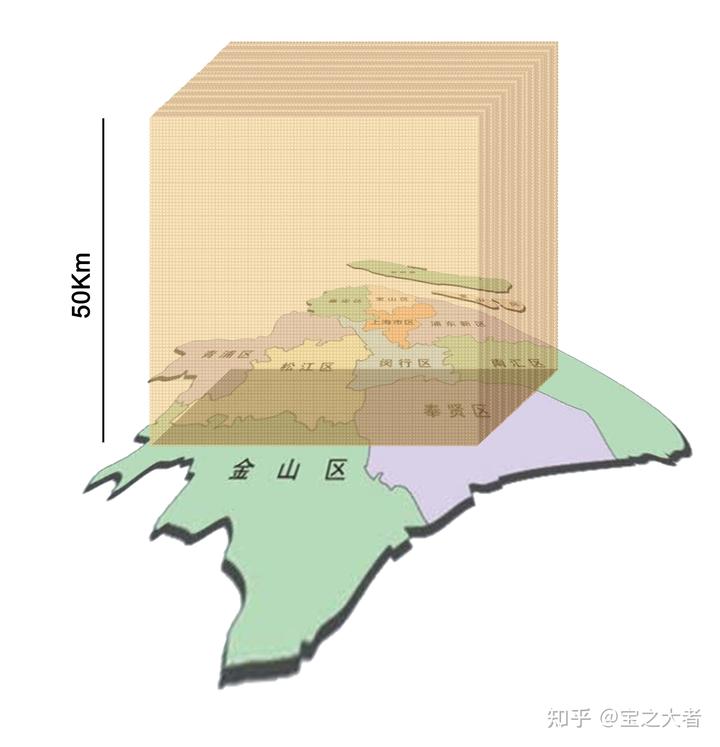
这是一个边长 50Km 的巨大沙块。

它与上海直接接触的面积达到 2500 平方千米，而上海市的面积是 6340 平方千米。

我对象住金山，所以我特别当心，尽量不压到金山区的人民。

如果你有讨厌的人，住在上海，可以私信我帮你压死他。

值得一提的是，这个沙块已经可以在卫星轨道被人眼直接看见了。

或许有人嫌我啰嗦了，但是对不起，是你们自己想要直观地感受大数。

而且，我们还远远没有来到大数的范畴。

因此我们得赶紧启程了，下一个目标：

！

来吧！

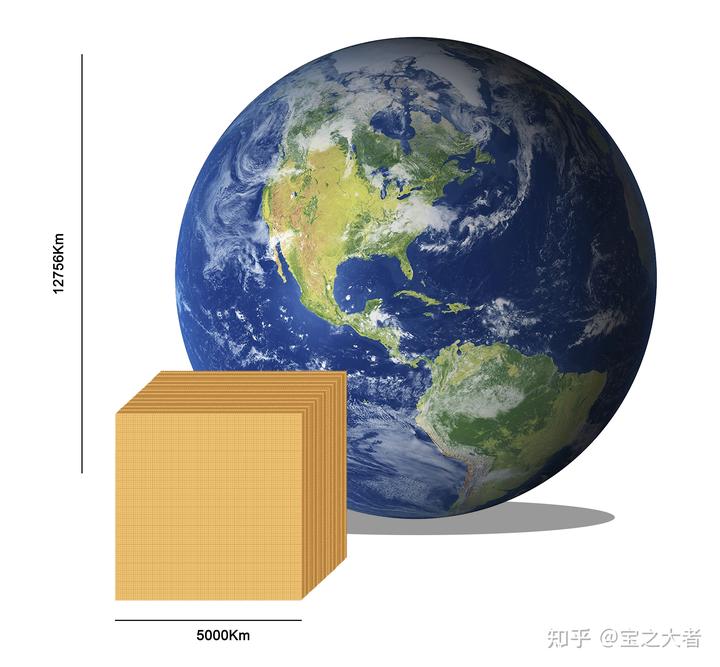
终于，地球上所有的沙子也不够用了。

因此这

个沙子，其中 90%都是贷的。

反正挂都开了，无所谓了。

我也懒得和你说这是多少千米巴拉巴拉，有多重巴拉巴拉。

你只需要知道特别大，特别重就好了，足够了。

OK，快马加鞭，继续来看

。

好家伙，我们的沙块快要赶上太阳的大小了，简直逆天。

必须提一嘴，为了看清地球月球，这张图里的哥俩被我画大了一点。

真实比例下，图中的地球和月球都会小到几乎看不见。

毕竟地球和月球之间的距离足以放下太阳系八大行星。

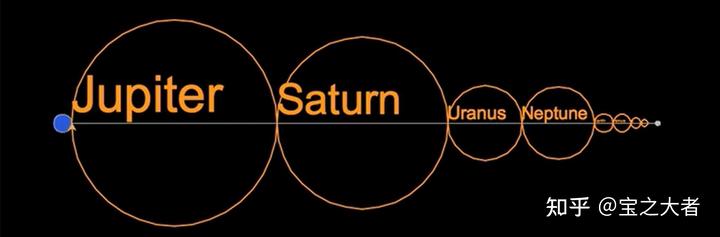
同时，我们不得不停下来讨论一下。

的沙块已经拥有了非常惊人的大小。

它的质量同样惊人，是

千克，而太阳是

千克。

换言之它已经有了 1/4 个太阳的重量。

不出意外的话，当我们到下一站的时候，它就已经会坍缩成一个黑洞了。毕竟等重量的黑洞的史瓦西半径比它还大。

不过这是一个数学话题，我们将无视一切物理定律。

前进，前进，不择手段地前进！

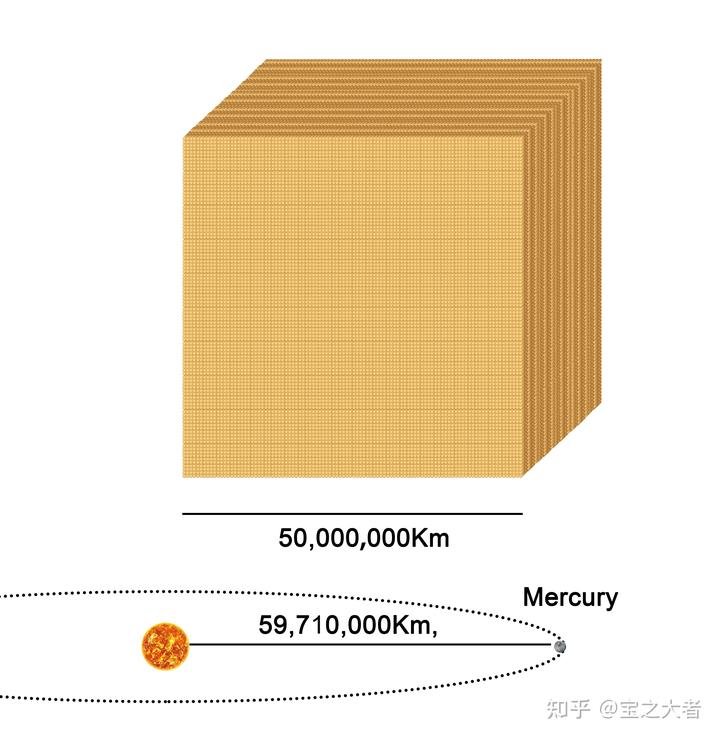
来了，这是

个沙子，同样的，太阳和水星被我画大了，原因同上。

我们的沙块有 25 万太阳的质量，也就是

Kg

这是计算黑洞史瓦西半径的公式，G 是万有引力常数，c 是逃逸速度（光速）。

代入可得

m

已经超过现在的沙块边长

m

很好，这玩意果然已经是个黑洞了。

没办法，让我们继续吧。

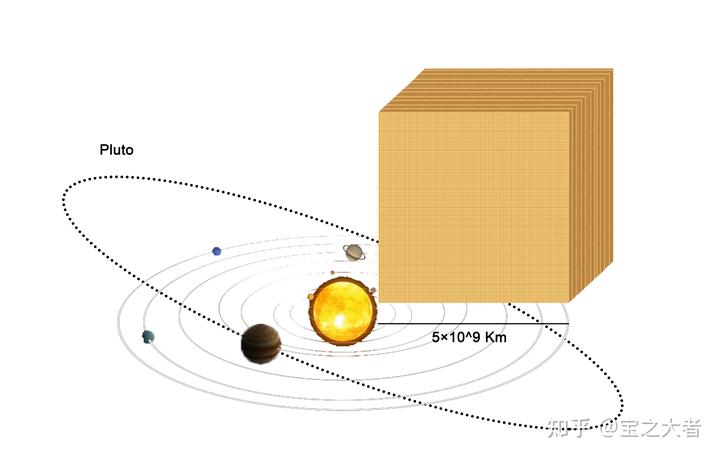
我的朋友们，我们即将告别常规天体的舞台。

因为这个

沙块的边长达到了可怕的 50 亿千米，我不得已在图中使用了科学计数法。

这已经超越了迄今为止人类观察到的最大的恒星盾牌座 UY 的大小，后者的直径是 23.79 亿千米。

巨大的沙块边长甚至达到了冥王星的轨道半径。

这是什么概念呢？

飞机的巡航速度是 832Km/h，就按时速 900 公里算吧。

如果你坐着这样一架飞机，从沙块的一个角飞往最近的另一个角。

这需要耗费 634 年的时间。

流浪地球计划需要 2500 年，你这也不赖，高低封个流浪沙雕计划。

还没到休息的时候。

来吧，

的沙块来了。

这是一个边长

Km 的沙块，这个距离约为 0.0529 光年。

你也别坐飞机了，你就是光速也得 20 天才能飞过去。

让我们跳跃一下，直接看

的沙块，边长将是

Km，或者说 5.29 万光年。

银河系的直径是 10~18 万光年。

所以直观地看就是这样：

也不啰嗦本星系群和室女座超星系团了，毕竟大多数人不了解。

花半天时间讲，到最后还是不直观。

直接来吧，让我们看看塞满整个宇宙需要多少沙子？

可观测宇宙的直径是 930 亿光年，也就是

Km。

如果我们用

，沙块的边长将是

Km

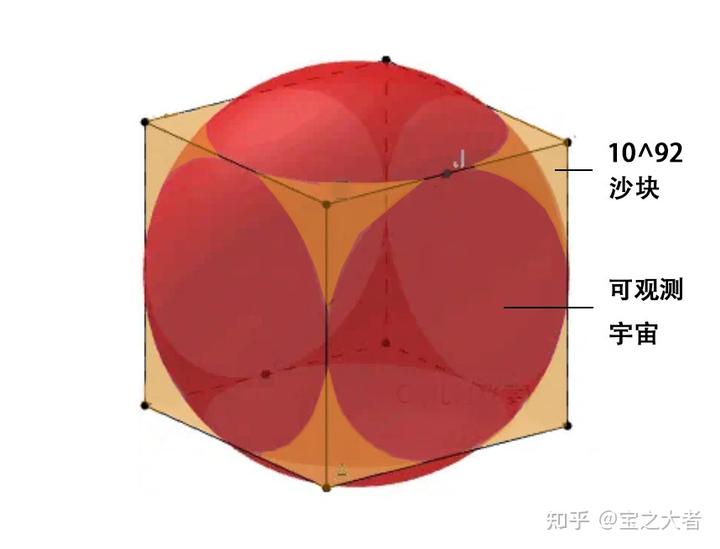
因此我们需要用到

粒沙子，此时我们的沙块边长是可怕的

Km

综上所述，理论上，整个宇宙都无法装下

粒沙子。

当然了，这里指的是可观测宇宙，因为我们无法确定宇宙在扩张热寂还是在收缩重启。

同时必须认识到，

其实早已远远超出宇宙中的基本粒子数目

。

这是因为太空太空了，所以这倒不值得大惊小怪。

有什么感想吗？

纵横无极为宇，古往今来为宙。但是这也太小了，小到甚至装不下

粒沙子。

而此刻我们即将迎来一个伟大的数字，它象征着大数领域的开端。

古戈尔数。

古戈尔数是

，它是美国数学家爱德华为了向侄子说明巨大，而与侄子一起发明的大数。

古戈尔有多大？

直观地看，它有这么大：

10,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000,000。

对于可以被直接写出来的大数，我们一般统称为垃圾。

但是别忘了，即便这个垃圾，也超越了宇宙的尺度。

怎么去感受古戈尔数呢？

我们必须再一次用

粒沙子把宇宙填满。

并且，从此刻起，每粒沙子都由 1 千万（

）个“小沙壁”组成。

那么，我们的宇宙里，将有

个小沙壁。

你也别管啥是“小沙壁”，反正是规定出来的。

古戈尔数只是一个垫脚石。

谁的垫脚石？古戈尔普勒克斯的垫脚石，后者是：

，也就是以 10 为底，古戈尔数为指数的数字。

也可以记作：

正如我们之前所提到的，古戈尔已经超越了宇宙里原子的总数。

因此在正常的宇宙里，古戈尔普勒克斯不能像古戈尔一样直接写出来（0 的数目无法写完）。

但是在我们的沙子宇宙里可以。

如果我们在每个“小沙壁”上写个 0（注意，每粒沙子包含 1000 万的小沙壁）

当我们写完所有

的沙子后，再写一个 1，我们将写完古戈尔普勒克斯。

我试过，大概 1 秒能写三个 0。

但是只靠宝之大者是不够的，我们需要更多人手。

整个人类史，加上智人，大概有 1150 亿人曾经在地球上活过。

人数不少了吧，但是我们还需要更极端一点。

所有人都从出生起开始写 0，并且一天工作 24 小时，并且强迫所有人活到 80 岁才能死。

（撒旦听了直呼人间才是地狱）

每个人一生将可以写 3×60×60×24×365×80=7568640000 个小沙壁。

这大概是 750 粒沙子。

那么我们全人类将可以写掉

粒沙子。

这大概是一个边长 21m 的立方体。

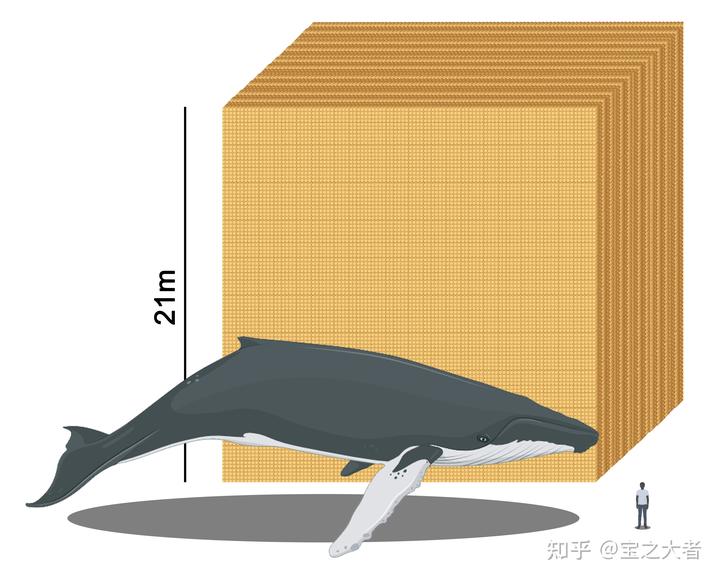
真亲切，又看到人类尺度的东西了。

然而别忘了，沙子遍布整个宇宙，而我们仅仅完成了一个 21×21×21 的立方体。

也就是说，即便全人类一秒都不休息，从出生的那一刻起每秒都在写 0。

最终也没能写完古戈尔普勒克斯。

说得更确切一点，古戈尔普勒克斯已经是超越了现实意义的大数，并且无法被人类认知直接感受。

而理解古戈尔普勒克斯的巨大，仅仅是我们扣响葛立恒数大门的准备。

毕竟和真正的大数相比，古戈尔普勒克斯实在有点费拉不堪。

不科普高德纳箭头了，直接从

说起。

90%的人了解葛立恒数，只能了解到

有多大，后面开始就变成听天书了。

这不奇怪，因为

确实是一个分水岭。

大多数文章讲完

就会开始说

，而后者

，这太跳跃了

在这篇经典的文章里^[1]，

被称为“爆太阳菊”，十分形象。因为这个指数塔的高度写完以后可以戳到太阳。

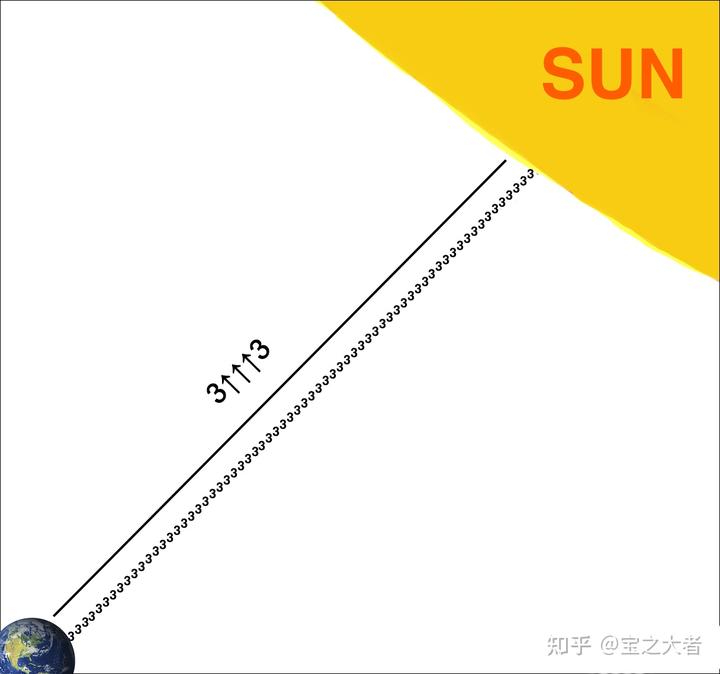
也别纠结比例了，首先我就写不下 7.6 万亿个 3，图中也就写了 60 个 3。

“爆太阳菊”是一个无法形容的超大的数字，甚至毫不夸张地说，90%的挑战葛立恒数的人都未能超越它。

因此，如果说完

就开始说

只能让读者知道 G（1）很大，大得不可想象，葛立恒数更大，大得难以言喻。

但是究竟有多大就不知道了。

不妨停下来思考一下，

是 7.6 万亿，那么，

有多大？

直观上应该大不了多少吧？

让我们检查一下：

7.6 万亿

22.8 万亿

如果你听过“指数爆炸”这个名词，你就会知道指数的增长将引起数值的巨大改变。

（宇宙中原子的总数）

仅仅从 28 增加到 168，就又一次突破了宇宙的尺度。

那么，

得有多大？更进一步的，

有多大？

反正挂已经开了，直接来吧，

得有多大？

为什么突然冒出这么个不丁不八的数字？因为这 tm 的就是

的数值。

它有多大？它是一个 3.6 万亿位的数字。

明白了吗？为什么别人只告诉你

而不讲

？因为前者已经是能直接被写出来并理解的最后一个数字了。

还记得古戈尔数吗，那个长得不得了的东西。

古戈尔

仅仅 3 层的指数塔，就把曾经为了定义大数而发明的古戈尔侮辱。

那么曾经那个不可一世的古戈尔普勒克斯呢？

那个全人类一起在沙子上写 0，最终都只能徒呼负负的古戈尔普勒克斯呢？

坦白地讲，

确实还杀不了古戈尔普勒克斯。

但是我们只需简简单单的把数字改成 5，后者就也得接受被侮辱的命运。

古戈尔普勒克斯

指数塔仅仅增加一层，带来的是毁天灭地的改变。我没法向你说明

有多么地碾压古戈尔普勒克斯。

如果用比尔盖茨之于我的存款来比喻，仍旧是在侮辱

之于古戈尔普勒克斯。

有的人会说，怎么老是侮辱别人？

没办法，指数塔这鬼东西就是不讲理。毕竟所谓不可一世的古戈尔普勒克斯，用指数塔表示也无非就是

，一个只有 3 层的指数塔。

在大数的领域，往往不存在针锋相对，亦或是旗鼓相当。有的，就只有侮辱，把你摁在地上踩成齑粉的侮辱。

所以，根本不需要什么

，区区一个

已经凌虐人类的认知，践踏人类的想象。

而

之于

是什么样子？

让我们直观地画出爆太阳菊的

和

。

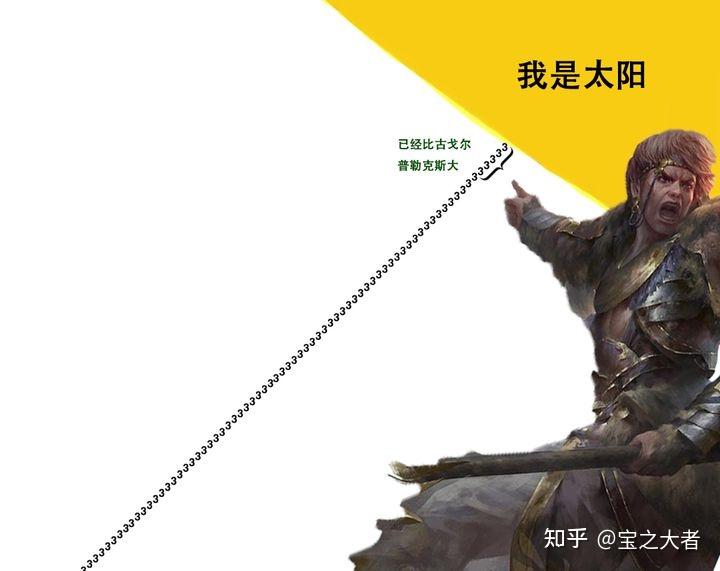
只是地球到太阳这个距离的几厘米长的部分。实在是微不足道。

不妨构造函数

当 x=1 的时候，结果就是 3，很小。

当这个 x 是 2 时，结果是 27 也不大。

但是 x=3 的时候，结果就已经是 7.6 万亿。

x=4 的时候，它可以侮辱古戈尔。

x=5 的时候，它侮辱古戈尔普勒克斯。

当 x=7.6 万亿的时候，它真就想侮辱谁侮辱谁。而这个结果，就是大名鼎鼎的爆太阳菊。

至此，我们才仅仅是感受了葛立恒数的计量单位“爆太阳菊”的战斗力，这还仅仅是

。

仅仅一个计量单位，已经突破了人类认知的极限。

事情有多离谱？打个比方的话，就是你接受了 5 分钟的搏击训练后，教练说要给你安排一个离谱的对手，是外国人。

你寻思了一下：有多离谱，泰森啊？

教练摇摇头：不是，灭霸。

同样的，讲完

就讲

同样太过于跳跃了。

我必须先说说

。

这个括号里面的就是我们熟悉的 “爆太阳菊”，这次它变成了指数塔的层数。

层数！太可怕了！是层数！如果 7.6 万亿的高度是爆太阳菊，那爆太阳菊的高度绝对可以爆古戈尔普勒克斯个…古戈尔普勒克斯个可观测宇宙（括号里可以有古戈尔普勒克斯个，反正仍然弗如远甚）

我头一次觉得现代汉语的词汇是如此匮乏，缺乏一个可以直接把读者吓疯的成语。而这个成语才是我需要的

再看一眼我们的函数，

当 x=7.6 万亿的时候，f（x）的结果是

（也就是爆太阳菊）就已经大得无法无天。

这次是把爆太阳菊当成 x 输入进去，出来的结果（

）已经无法找到合适的汉语词汇来形容了。

然后，如果把无法形容当成 x 输入进去，出来的结果就是

，这尼玛已经只能用荒谬无稽来形容了。

如果你能理解我在说什么，那就接着往下看，不然就听个结论也行。

就这样，我们一层一层地套娃，反正 f（x）的结果早就已经不能形容。每次迭代的结果都能侮辱输入进去的数字。而任何一个输入进去的数字都超越人类的认知。

上面说的这个恐怖的迭代，其实就是在

这个函数的基础上令 x 的数值 +1。

有没有感受到箭头数增加的可怕？仅仅 3 个箭头的运算级别，就能产生天翻地覆的变化。

终于，我们该看看

有多大了

也就是把爆太阳菊

直接输入到

这个函数里

当把

输入进去的时候，

爆太阳菊

现在是直接把爆太阳菊输入进去了。

注意，不是把爆太阳菊输入到

里，要多整整一个箭头。

什么概念？还记得我们上面的迭代过程吗？每次把上次的结果当做输入的 x，再得出一个 f（x）的这个迭代。

G（1）的概念，就是要我们迭代爆太阳菊次。

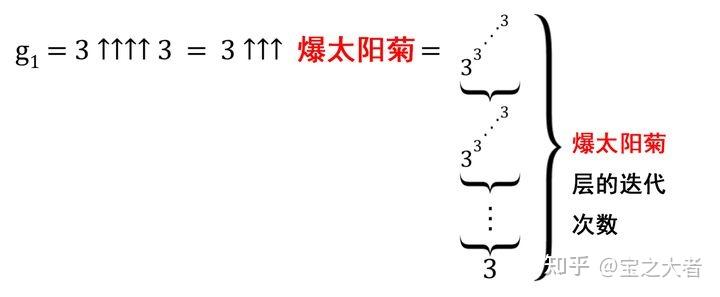
这个迭代的过程需要重复

次，甚至连次数人类也不能理解。

毕竟人类能理解的领域，就到

为止了，多一层都不行了。

至此，你已经勉强窥见 G（1）的一鳞半角。

想要用宇宙堆沙子的方式让人类理解古戈尔普勒克斯都不是一件易事，而小小的

就已经把古戈尔普勒克斯侮辱了。

更可怕的是，对葛立恒数而言，G（1）甚至是最温柔的一层。毕竟所有的省略号仅仅代表迭代的次数。

而 G（2）开始，可就是箭头数了。

G（1）一共 4 个箭头就已经令人抓狂了，而 G（2）的箭头数是 G（1）。

真的是妈妈的弟弟去世，没舅了。

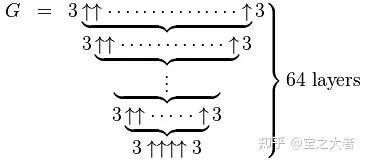
很遗憾，讲到后面，仍然无法让读者直观感受葛立恒数。

但笔者相信，目前不存在让人类直观感受葛立恒数的手段。

葛立恒数就只应该存在于数学的理论之中。

本文用宇宙堆沙子的方式进行描述，不是因为这样可以让读者直观感受葛立恒数，是为了让读者充分理解为什么无法直观感受葛立恒数。

最后，感谢阅读完全文的读者。

这篇文章从作图到行文，我耗时 7 个多小时，现在是凌晨 4 点 11，累死我了。