除了黎曼猜想，数学界还有哪些至今尚未得到证实的猜想？

高斯圆问题，又叫圆内整点问题。很容易懂，很难证明。我在之前的这篇里面也写过：

PENG Bo：黎曼猜想为何这样难证？幻想的证明思路以及 Atiyah 论文

而且它有个优点，它有一个数字可以让你不断改进，所以能改进一点也是贡献。

首先，我们在格点纸上画个半径为 r 的圆，里面当然大致就有

个格点。

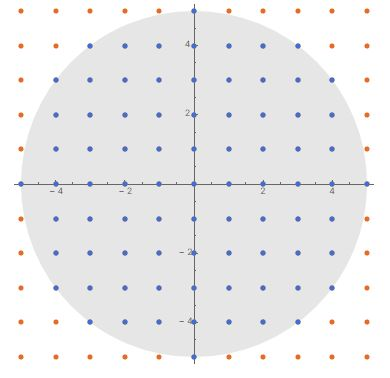
令 N(r) 为实际的格点数。那么所谓误差项 E(r) 是这样定义的：

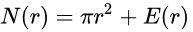
现在的关键是，能否对这里的误差 E(r) 有更精确的估计？高斯证明了：

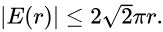
这是因为，大致来说，误差肯定小于圆的周长（这是很漂亮的几何观点，其实 class number formula 就是这样来的），大家可以自己试试证明这个。

但是，圆很规则，所以，实际上误差更小，目前大家猜是：

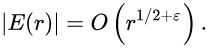
用模形式的方法（Voronoi summation），可以证明

的情况，现在最好的结果可以证明到

。

而 131/208=0.6298...，所以离 0.5+epsilon 还很远，一百年的时间只前进了 0.05。如果你能改进这个数字，就可以发论文。

高斯圆问题，看上去很人畜无害，但是非常难。如果你能证明 0.5+epsilon，你的方法肯定可以用于数论中的许许多多其它领域。

===========================

欢迎看我在知乎的更多回答：

PENG Bo：我在知乎的回答&文章整理：数学 / 物理篇

最近还刚出版了一本人工智能深度学习的书，感兴趣的同学欢迎关注：

PENG Bo：我在知乎的回答&文章整理：AI/ 编程 / 金融 / 八卦篇PENG Bo：我在知乎的回答&文章整理：文 / 艺 / 音 / 生活篇