矩阵的本质是什么？

这篇回答节选自我在专栏《机器学习中的数学：线性代数》中的一篇文章，我们从矩阵乘法运算为一个切入点，来谈谈矩阵的本质含义。

欢迎关注我的知乎账号 @石溪 ，将持续发布机器学习数学基础及算法应用等方面的精彩内容。

1.回顾矩阵的乘法运算

1.1.矩阵的数量乘法

矩阵的数量乘法，描述起来也非常简单：

同样，我们看一个代码的例子：

代码片段：

import numpy as np  A = np.array([[1, 2, 3],                [4, 5, 6]])  print(2*A)  

运行结果：

[[ 2  4  6]   [ 8 10 12]]  

1.2.矩阵与矩阵的乘法

矩阵与矩阵的相乘，过程要稍微复杂一点，因此我们拿出来单讲。例如下面举例的矩阵

和矩阵

的乘法运算，对两个矩阵的形态是有要求的。

仔细观察这个计算公式，我们总结出以下的一些要求和规律：

1 左边矩阵的列数要和右边矩阵的行数相等

2 左边矩阵的行数决定了结果矩阵的行数

3 右边矩阵的列数决定了结果矩阵的列数

同样，我们用

来演示下面这个例子：

代码片段：

import numpy as np    A = np.array([[1, 2],                [3, 4],                [5, 6]])  B = np.array([[3, 4, 5],                [6, 7, 8]])    print(np.dot(A, B))  

运行结果：

[[15 18 21]   [33 40 47]   [51 62 73]]  

2.改变空间位置：矩阵乘以向量的本质

矩阵与向量的乘法，一般而言写作矩阵

在左，列向量

在右的

的形式。这种

的写法便于描述向量

的位置在矩阵

的作用下进行变换的过程（下面会详细介绍）。

矩阵与向量的乘法，其实可以看作是矩阵与矩阵乘法的一种特殊形式，只不过位于后面的矩阵列数为 1 而已。

我们对照前面讲过的矩阵与矩阵的乘法，来对比一下矩阵与向量的乘法规则，我们把列向量看作是列数为 1 的特殊矩阵，那么就会非常明确：

1、矩阵在左，列向量在右，矩阵的列数和列向量的维数必须相等

2、矩阵和向量相乘的结果也是一个向量

3、矩阵的行数就是最终结果输出的列向量的维数

4、乘法的规则如上所示，就是矩阵的每行和列向量进行对应元素分别相乘后相加

我们来看一个矩阵与列向量相乘的例子：

代码片段：

import numpy as np  A = np.array([[1, 2],                [3, 4],                [5, 6]])  x = np.array([[4, 5]]).T    print(np.dot(A, x))  

运行结果：

[[14]   [32]   [50]]  

从结果看，原始向量表示二维空间中的一个点，坐标为

，经过矩阵

​乘法的作用，转化为三维空间中坐标为

的点。

因此从这个例子中我们可以总结一下矩阵的作用：在特定矩阵的乘法作用下，原空间中的向量坐标，被映射到了目标空间中的新坐标，向量的空间位置（甚至是所在空间维数）由此发生了转化。

关注 @石溪 知乎账号，分享更多机器学习数学基础精彩内容。

3.从行的角度思考

学习了矩阵、向量的表示方法以及运算规则之后，我们回过头来静静的思考一个问题：矩阵

和列向量

的乘法

到底意味着什么？下面，我们就来挖掘一下这里面的内涵。

在二阶方阵

与二维列向量

相乘的例子中，

。

刚才说了，位于矩阵

第

行的行向量的各成分和列向量

各成分分别相乘后相加，得到的就是结果向量的第

个成分。这个计算方法有没有感觉很熟悉？没错，这不就是向量点乘的定义式么？

即：

]。

矩阵与向量的乘法如果从行的角度来看，就是如此。常规的计算操作就是这么执行的，但是似乎也没有更多可以挖掘的，那我们试试继续从列的角度再来看看。

4.列的角度：重新组合矩阵的列向量

如果从列的角度来计算矩阵与向量的乘积，会有另一套计算的方法，可能大家对这种方法要相对陌生一些。但是实质上，这种方法从线性代数的角度来看，还要更为重要一些，我们还是用二阶方阵进行举例。

发现了规律没有？我们通过这种形式的拆解，也能得到最终的正确结果，这就是从列的角度进行的分析。从前面的知识我们可以这样描述：从列的角度来看，矩阵

与向量

的乘法是对矩阵

的各列向量进行线性组合的过程，每个列向量的组合系数就是向量

的各对应成分。

这么理解似乎有点新意，我们按照列的思想重新把矩阵

写成一组列向量的形式：

依照上述公式，我们举一个实际的例子，就更清楚了。

所得到的结果就是矩阵第一列的列向量

的 3 倍加上第二列列向量

的 5 倍。

因此，一个矩阵和一个向量相乘的过程，就是对位于原矩阵各列的列向量重新进行线性组合的过程，而线性组合的各系数就是向量的对应各成分。

5.进一步引申：变换向量的基底

5.1.二阶方阵与二维列向量乘法举例

为了方便说明原理，我们依旧用二阶方阵

与二维列向量

的乘法进行举例：

二维列向量

的坐标是

和

，还记得之前我们介绍过的向量坐标的概念么？向量的坐标依托于基底的选取，向量坐标在基底明确的前提下才有实际意义，而这个二维列向量，我们说他的坐标是

和

，基于的就是默认基底：(

和

。那么二维列向量的完整表达式就是：

。

好，回顾了这些基础，我们就利用他将矩阵与向量的乘法表达式做进一步的展开：

是不是已经初见端倪了？我们再直观的展示一下式子首尾的结果，在矩阵

的乘法作用下，向量完成了下面的转换：

挑明了说，就是矩阵把向量的基底进行了变换，把旧的基底 (

,

)变换成了新的基底(

,

)。

映射前由旧的基底分别乘以对应的坐标

来表示其位置，而映射后，由于旧的基底映射到新的基底，那向量自然而然应该用新的基底来分别乘以对应坐标

来描述改变后的空间位置，

，如图 1 所示。

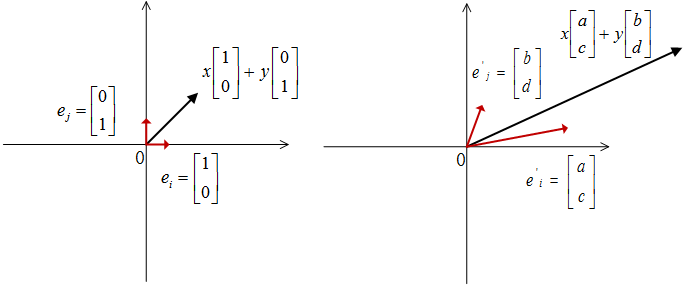
5.2.矩阵的各列就是映射后的新基底

结合矩阵的式子我们不难发现：矩阵

的第一列

就是原始的默认基向量

变换后的目标位置（新的基向量），而第二列

就是另一个基向量

映射后的目标位置（新的基向量）。

基底的变换明确了，那向量的坐标呢？映射后得到的新向量，如果以 (

,

)为基底，他的坐标仍是

，如果以默认的(

,

)为基底，那么其坐标就是

。

5.3.扩展到三阶方阵

为了让结果更让人信服，我们再看看三阶方阵和三维列向量相乘的例子，同理也满足这个过程：

是不是和二阶矩阵的情况是一模一样呢？三阶方阵将三维列向量的基底做了映射转换，方阵的第一列

​是原始基向量

​映射后的目标位置（新的基向量），方阵的第二列

​是原始基向量

​映射后的目标位置（新的基向量），方阵的第三列

​是原始基向量

​映射后的目标位置（新的基向量）。

因此同样的，映射后的目标向量如果在新的基底

下看，其坐标仍然是

。如果放回到原始基底

下看，将新的基底

和他对应的坐标

相结合，就能得到默认原始基底下的坐标：

​ 。

5.4.一般化的：矩阵乘以维列向量

此处，我们看到的就是最一般的情况了，矩阵

​和向量

进行相乘。

在

矩阵

的作用下，原始的

维基向量

​映射成了新的基向量：

，

维基向量

​映射成了

​ ，我们发现，在这种一般性的情况下，如果

，那么映射前后，基向量的维数甚至都可能发生变化，

维列向量

变换成了

个

维列向量线性组合的形式，其最终结果是一个

维的列向量。

由此看出，映射后的向量维数和原始向量维数的关系取决于

和

的关系，如果

，那么目标向量的维数就大于原始向量的维数，如果

，那么目标向量的维数就小于原始向量的维数。

6.基变换的意外情况

实质上，如果仅仅停留在上面的讨论结果，那可能会显示出我们思考问题不够全面、准确。首先，“经过矩阵变换，会将原始的基底变换成为一组新的基底”这句话的表述就并不准确，之前这么说只是为了方便大家理解并建立概念。

为什么这么说呢？对于一个

的矩阵

和

维列向量

，经过

的乘法作用，

的

个

维默认基向量构成的基底被转换成了

个

维的目标向量。

当

的时候，这

个向量线性相关，因此不构成基底；

当

的时候，即使这

个向量线性无关，由于他们不能表示

维空间中的所有向量，因此也不能称之为基底；

当且仅当

，且这

个向量线性无关的时候，他们才能称之为一组新的基底。

不过即便有这些意外情况，我们这一讲里讨论的内容仍然具有重要意义，矩阵

的各列向量是

默认基底经过转换后的目标向量，正因为其在维度和线性相关性方面存在各种不同情况，因此这组目标向量的张成空间和原始向量所在的空间之间，就会存在多种不同的对应关系，这便是我们后续将要重点讨论的空间映射相关内容。