有没有符合 f'(x)=f(x+1) 的函数？

题目要求导数是原函数的平移，且平移量为 1。三角函数

就具有这类性质，但平移量为

。指数函数

也具有类似的性质，但平移量为 0。

考虑设计一个指数函数与三角函数相乘的函数，比如

其导数为

原函数平移 1 个单位

两式对比可以得到

问题来了，怎么解这个方程组呢？

第二个式子乘以虚数单位 i，然后两式相加，可以得到

记

，也就是解方程

.

这个方程在复数域内的解与朗伯 W 函数(Lambert W Function) 有关，其解有无数多个，可以表示为

(k 为任意整数)

用 MATLAB 计算的得到的数值解。比如，取 k=0, 此时 a = 0.318131505204764,b = 1.337235701430689.

z = -lambertw(0,-1)  % z = 0.318131505204764 - 1.337235701430689i  

画出原函数及其导数的图像

a = real(z);  b = imag(z);  f = @(x) exp(a*x).*sin(b*x);  df = @(x) a*exp(a*x).*sin(b*x) + b*exp(a*x).*cos(b*x);  fplot(f)  hold on  fplot(df)  grid on  legend('f','df')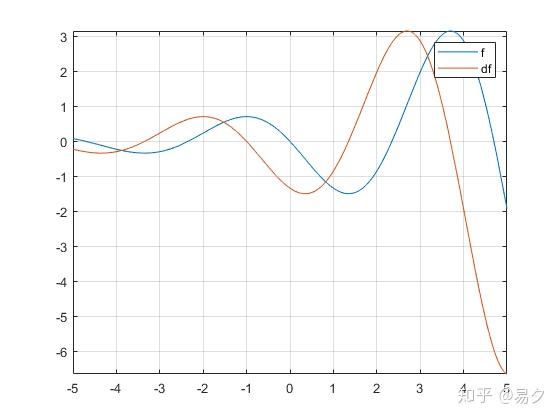  

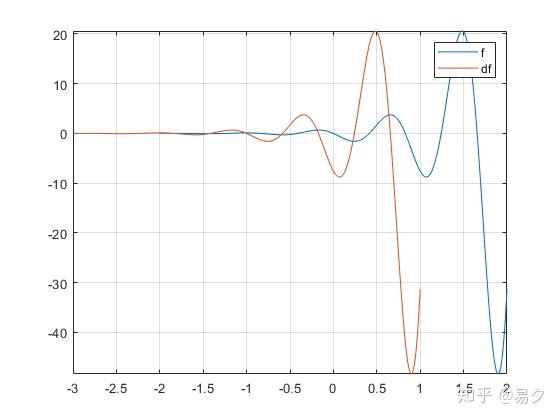
当 k 取其它整数时，也可以得到满足条件的其它函数，比如 k = 1 时，a = 2.062277729598284 ,b = - 7.588631178472513,此时函数图像如下所示