群论中最令你惊艳的结论是什么？为什么？

群论中最令人感到惊艳的结论当属

有限单群分类定理：每个有限单群都同构于下列单群中的一个：

素数阶循环群

交错群

有限 Lie 型单群（16 种）

典型群：

例外群：

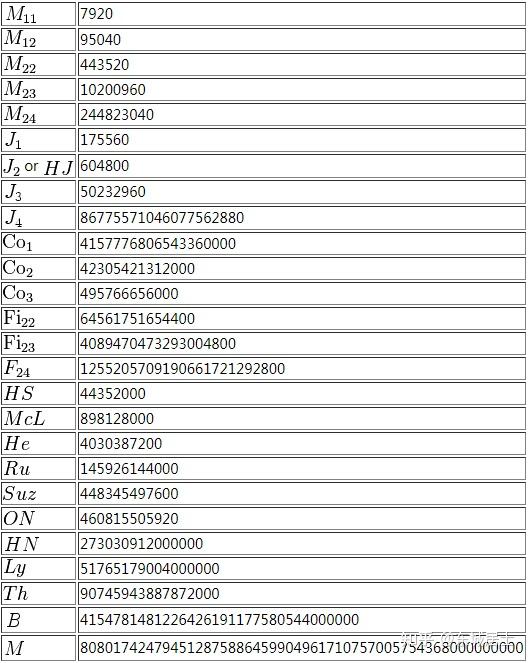
零散单群（26 个）

Mathieu 群：

Janko 群：

Conway 群：

Fischer 群：

Fischer 群的导出子群：

Higman-Sims 群：

McLaughlin 群：

Held 群：

Rudvalis 群：

Suzuki 零散群：

O'Nan 群：

Harada-Norton 群：

Lyons 群：

Thompson 群：

小魔群：

魔群：

注：单群的数量虽然很多，但它们大部分都是一些特定对象的对称群.

有限 Lie 型单群中的典型群（7 种）

有限 Lie 型单群中的例外群（9 种）

零散单群的阶都比较大，其中阶最大的是著名的魔群

其阶为

魔群其实是一个

维交换非结合代数的自同构群.

有限单群的分类是二十世纪群论研究中的一个重大工程. 从 1899 年 Burnside 的 On a class of groups of finite order 算起，到 2004 年 Aschbacher 和 Smith 的 The classification of quasithin groups，有限单群分类定理 的证明历时上 百年 由 数百篇 共 上万页 的论文组成！有限单群分类定理 证明的简化工作目前还在进行中，据说会在 2023 年完成.

Aschbacher 和 Smith 长达 1200 页的论文就算拿来当书都属鸿篇巨著了！